ADDING TWO FRACTIONS WITH DIFFERENT DENOMINATORS
We can use one of the following methods to add two fractions with different denominators.

Cross-Multiplication Method - Example
If the denominators of the fractions are co-prime or relatively prime, we have to apply this method.
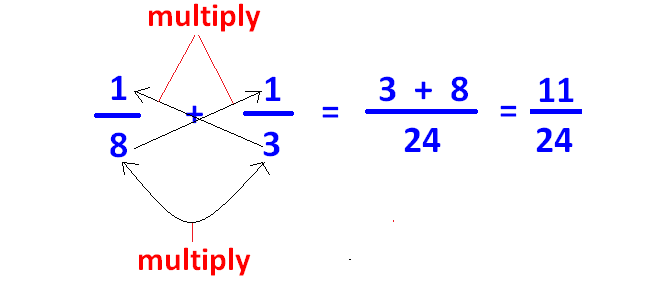
Fro example, let us consider the two fractions 1/8, 1/3.
In the above two fractions, denominators are 8 and 3.
For 8 and 3, there is no common divisor other than 1.
So 8 and 3 are co-prime.
Here we have to apply cross-multiplication method to add the two fractions 1/8 and 1/3 as given below.
LCM Method - Example
If the denominators of the fractions are not co-prime (there is a common divisor other than 1), we have to apply this method.
Fro example, let us consider the two fractions 5/12, 1/20.
In the above two fractions, denominators are 12 and 20.
For 12 and 20, if there is at least one common divisor other than 1, then 12 and 20 are not co-prime.
For 12 & 20, we have the following common divisors other than 1.
2 and 4
So 12 and 20 are not co-prime.
In the next step, we have to find the LCM (Least common multiple) of 12 and 20.
To find the LCM of 12 and 20, divide both 12 and 20 by the greatest common divisor as shown below.
The greatest common divisor of 12 and 20 is 4.
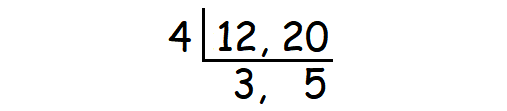
LCM is the product of the divisors and undivided numbers.
Therefore, LCM of 12 and 20 is
= 4 ⋅ 3 ⋅ 5
= 60
Now, make the denominators of both the fractions as 60 using multiplication and then add them.
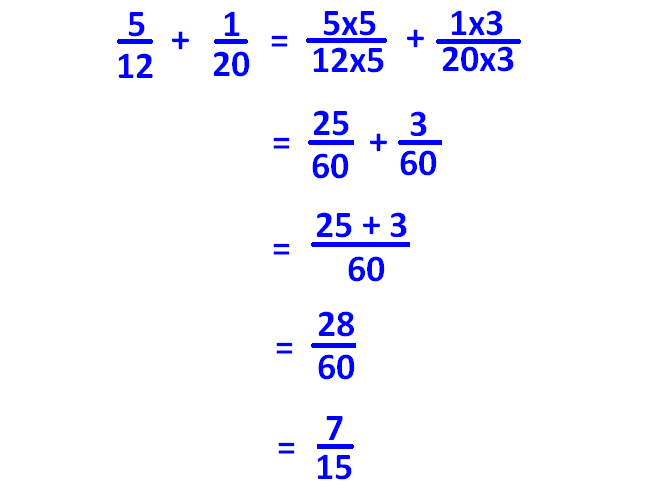
Problem 1 :
Add :
1/12 + 1/16
Solution :
The given two fractions are unlike fractions. Because, they have different denominators.
For 12 and 16, we have the following common divisors other than 1.
2 and 4
So 12 and 16 are not co-prime.
In the next step, we have to find the LCM (Least common multiple) of 12 and 16.
LCM of (12 and 16) = 48
Now, make the denominators of both the fractions as 48.
To make the denominator of both the fractions as 48 , we have to multiply the numerator and denominator of the first fraction by 4 and the second one by 3.
Then, we have
1/12 + 1/16 = 4/48 + 3/48
= (4 + 3)/48
= 7/48
So, the sum of the two fractions is 7/48.
Problem 2 :
Add :
3/20 + 7/30
Solution :
The given two fractions are unlike fractions. Because, they have different denominators.
For 20 and 30, we have the following common divisors other than 1.
2, 5 and 10
So 20 and 30 are not co-prime.
In the next step, we have to find the LCM (Least common multiple) of 20 and 30.
LCM of (20 and 30) = 60
Now we have to make the denominators of both the fractions as 60.
To make the denominator of both the fractions as 60, we have to multiply the numerator and denominator of the first fraction by 3 and and for the second fraction by 2.
Then, we have
3/20 + 7/30 = 9/60 + 14/60
= (9 + 14)/60
= 23/60
So, the sum of the two fractions is 23/60.
Problem 3 :
Add :
3/7 + 2/9
Solution :
The given two fractions are unlike fractions. Because, they have different denominators.
For 7 and 9, there is no common divisor other than 1.
So 7 and 9 are co-prime
Here, we have to apply cross multiplication method to add the two fractions.
To add the two fractions, we have to do the following three steps.
Step 1 :
Multiply the numerator of the first fraction by denominator of the second fraction.
Step 2 :
Multiply the numerator of the second fraction by denominator of the first fraction.
Step 3 :
Multiply the denominators of the two fractions.
When we do the above three steps, we will have
3/7 + 2/9 = (27 + 14)/63
= 41/63
So, the sum of the two fractions is 41/63.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Writing Quadratic Functions in Standard Form
Apr 26, 24 12:39 PM
Writing Quadratic Functions in Standard Form or Vertex Form -
Factoring Quadratic Trinomials
Apr 26, 24 01:51 AM
Factoring Quadratic Trinomials - Key Concepts - Solved Problems -
Factoring Trinomials Worksheet
Apr 25, 24 08:40 PM
Factoring Trinomials Worksheet
