ADDITION AND SUBTRACTION EQUATIONS

Example 1 :

Solve for x :

x + 7 = 8

Solution :

x + 7 = 8

Subtract 7 from each side.

(x + 7) - 7 = 8 - 7

x + 7 - 7 = 1

x = 1

Example 2 :

Solve for y :

y - 3 = 2

Solution :

y - 3 = 2

Add 3 to each side.

(y - 3) + 3 = 2 + 3

y - 3 + 3 = 5

y = 5

Example 3 :

Adding 7 to a number results 25. Find the number.

Solution :

Let x be the number. 

x + 7 = 25

Subtract 7 from each side.

(x + 7) - 7 = 25 - 7

x + 7 - 7 = 18

x = 18

Example 4 :

John had some candies. He gave 5 candies to his friend and now he has 18 candies. How many candies did John initially have ?

Solution :

Let m be the number of candies that John initially had. 

m - 5  = 18

Add 5 to each side.

(m - 5) + 5 = 18 + 5

m - 5 + 5 = 23

m = 23

John initially had 23 candies.

Example 5 :

The sum of two numbers 22.5. If one number is 7.5, find the other number.

Solution :

Let x be the other number.

x + 7.5  = 22.5

Subtract 7.5 from each side.

(x + 7.5) - 7.5 = 22.5 - 7.5

x + 7.5 - 7.5 = 15

x = 15

The other number is 15.

Example 6 :

18 is taken away from a number results 30. Find the number.

Solution :

Let x be the number.

x - 18 = 30

Add 18 to both sides.

(x - 18) + 18 = 30 + 18

x - 18 + 18 = 48

x = 48

The number is 48.

Example 7 :

If sum of two interior angles angles of a triangle is 120°, find the measure of the third angle.

Solution :

Let x be the measure of third angle.

Sum of the three interiors angles of a triangle = 180°

x + 120° = 180°

Subtract 120° from each side.

(x + 120°) - 120° = 180° - 120°

x + 120° - 120° = 60°

Measure of the third angle is 60°.

Example 8 :

In a right triangle, if one of the angles is 50°, find the measure of the third angle.

Solution :

Let x be the measure of third angle.

Sum of the three interiors angles of a triangle = 180°

x + 90° + 50° = 180°

x + 140° = 180°

Subtract 140° from each side.

(x + 140°) - 140° = 180° - 140°

x + 140° - 140° = 40°

x = 40°

Measure of the third angle is 40°.

Example 9 :

The perimeter of a triangle is 25 cm and sum of the lengths of two sides is 16 cm. Find the length of the third side.

Solution :

Let x be the length of the third side.

Perimeter = 25

x + 16 = 25

Subtract 16 from each side.

(x + 16) - 16 = 25 - 16

x + 16 - 16 = 9

x = 9

Length of the third side is 9 cm.

Example 10 :

The perimeter of an isosceles triangle is 35 cm. If the length of each of the two equal sides is 12 cm, find the length of the third side.

Solution :

Let x be the length of third side.

Perimeter = 35

x + 12 + 12 = 35

x + 24 = 35

Subtract 24 from each side.

(x + 24) - 24 = 35 - 24

x = 11

Length of the third side is 11 cm.

Example 11 :

The width of a rectangle is x cm. The length is 1.5 cm more than the width. The perimeter of the rectangle is 17 cm. Write down an equation satisfied by x and solve it to find x.

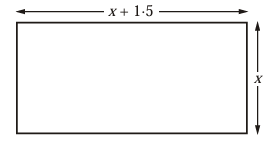
Solution :

Perimeter of the rectagle = 2(length + width)

Length = x + 1.5 cm

Width = x cm

Perimeter = 2(x + 1.5 + x)

= 2(2x + 1.5)

2(2x + 1.5) = 17

2x + 1.5 = 17/2

2x + 1.5 = 8.5

2x = 8.5 - 1.5

2x = 7

x = 7/2

x = 3.5 cm

Width = 3.5 cm

Length = x + 1.5 ==> 3.5 + 1.5 ==> 5 cm

So, length and width of the rectangle is 5 cm and 3.5 cm repsectively.

Example 12 :

The present age of father is four times the age of his son. After 10 years, age of father will become three times the age of his son. Find their present ages.

Solution :

Let the present age of son be x years

the present age of father = 4x years

After 10 years Age of son = (x + 10) years

Age of father = (4x + 10) years

According to the given condition

4x + 10 = 3(x + 10)

4x + 10 = 3x + 30

4x – 3x = 30 –10

x = 20

Present age of son = 20 years

and 

present age of father = 4x = 4 × 20

= 80 years.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.