ADDING INTEGERS ON A NUMBER LINE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
We can add numbers with same sign or different signs using a number line.
In the given two numbers, if the second number is positive, we have to move in the positive direction on the number line.
In the given two numbers, if the second number is negative, we have to move in the negative direction on the number line.
Example 1 :
Add 3 and 2 using a number line.
Answer :
Here, the integers 3 and 2 are having the same sign. That is positive.
To find the sum of integers 3 and 2, we have to start at 3
Because the second number '2' is positive, we have to move 2 units in the positive direction as given in the picture below.
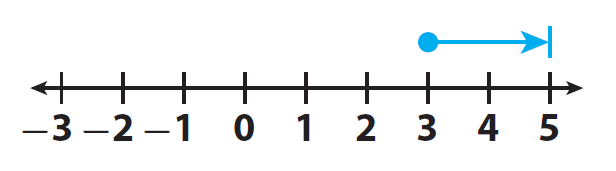
After having move 2 units in the positive direction, we are in the position of '5'.
So,
3 + 2 = 5
Example 2 :
Add 3 and -2 using a number line.
Answer :
Here, the integers 3 and -2 are having different signs.
To find the sum of integers 3 and -2, we have to start at 3
Because the second number -2 is negative, we have to move 2 units in the negative direction as given in the picture below.
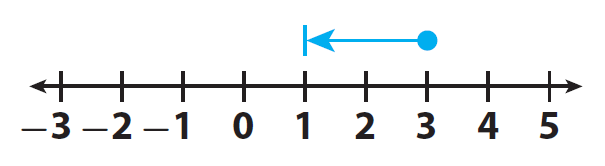
After having move 2 units in the negative direction, we are in the position of '1'.
So,
3 + (-2) = 1
Example 3 :
The temperature was 2°F below zero. The temperature drops by 5°F. What is the temperature now ?
Answer :
Step 1 :
According to the question, the initial temperature was 2°F below zero. 2 below zero is -2.
So, the initial temperature is -2°F
Step 2 :
Let us mark the initial temperature on the number line.
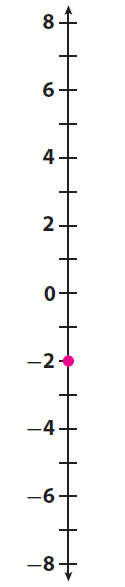
Step 3 :
A drop in temperature of 5° is like adding -5° to the temperature.
Because the temperature is dropping, we have to go below the initial temperature. The temperature drops by 5°. So, we have to count 5 units on the number line below -2 to find the final temperature.
That is -7.
Mark the temperature now on the number line.
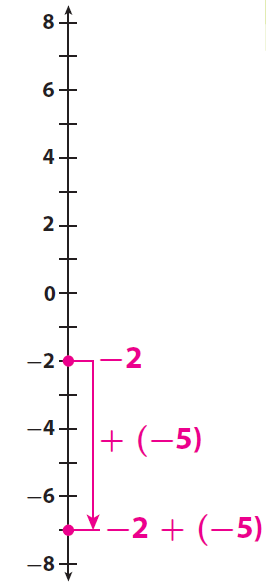
Step 4 :
From the above figure, the final temperature is -7°.
Justify and Evaluate :
In the above example, we have just added -2 and -5.
From the above example problem, it is clear that when we add two negative numbers, we have to add them as usual and take negative sign to the result.
Example 4 :
Suppose the temperature is -1°F and drops by 3°F. Explain how to use the number line to find the new temperature.
Answer :
Start at -1. Move 3 units in a negative direction to -4; the new temperature is -4 °F.
Example 5 :
How would using a number line to find the sum (2 + 5) be different from using a number line to find the sum -2 + (-5) ?
Answer :
Instead of starting at 2 and moving 5 units in a positive direction to get 7, you would start at -2, move 5 units in a negative direction, and get -7.
Example 6 :
What are two other negative integers that have the same sum as - 2 and - 5 ?
Answer :
Sample answer: - 3 and - 4
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 43)
Jan 04, 26 01:38 AM
10 Hard SAT Math Questions (Part - 43) -
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations
