ADDING INTEGERS WITH DIFFERENT SIGNS WORKSHEET

Problem 1 : 

Add (-4) and (+7). 

Problem 2 : 

Add (+5) and (-8). 

Problem 3 : 

Add (+1) and (-2). 

Problem 4 : 

Use model to add -4 and +3. 

Problem 5 :

Add 3 and -2 using a number line.

Detailed Answer Key

Problem 1 : 

Add (-4) and (+7). 

Solution : 

Step 1 : 

Find the absolute difference of the integers without the actual signs. 

|4 - 7|  =  |-3|  =  3

Step 2 : 

In the given two integers 4 and 7, the sign of the bigger integer is positive. So, we have to take positive sign to the answer. 

So,

(-4) + (+7)  =  +3

Problem 2 : 

Add (+5) and (-8). 

Solution : 

Step 1 : 

Find the absolute difference of the integers without the actual signs. 

|5 - 8|  =  |-3|  =  3

Step 2 : 

In the given two integers 5 and 8, the sign of the bigger integer is negative. So, we have to take negative sign to the answer. 

So,

(+5) + (-8)  =  -3

Problem 3 : 

Add (+1) and (-2). 

Solution : 

Step 1 : 

Find the absolute difference of the integers without the actual signs. 

|1 - 2|  =  |-1|  =  1

Step 2 : 

In the given two integers 1 and 2, the sign of the bigger integer is negative. So, we have to take negative sign to the answer. 

So,

(+1) + (-2)  =  -1

Problem 4 : 

Use model to add -4 and +3. 

Solution : 

Let us take four negative counters for -4 and three positive counters for +3. 

Mark zero pairs. 

In the above figure, if you remove three zero pairs, the result will be one negative counter. 

So, the answer is -1. 

Therefore,

(-4) + (+3)  =  -1

Problem 5 :

Add 3 and -2 using a number line.

Solution :

Here, the integers 3 and -2 are having different signs. 

To find the sum of integers 3 and -2, we have to start at 3 

Because the second number -2 is negative, we have to move 2 units in the negative direction as given in the picture below.

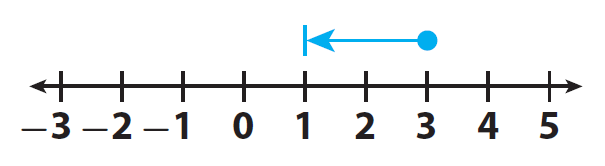
After having move 2 units in the negative direction, we are in the position of 1. 

Therefore,

3 + (-2)  =  1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.