ADDING AND SUBTRACTING REAL NUMBERS

All real numbers can be represented on a number line as shown below. 

A number line can be used to model addition and subtraction of real numbers. 

Addition :

To model addition of a positive number, move right. To model addition of a negative number, move left. 

Subtraction : 

To model subtraction of a positive number, move left. To model subtraction of a negative number, move right. 

Adding and Subtracting Numbers on a Number Line

Add or subtract using a number line. 

Example 1 :

-3 + 6

Solution :

On a number line, start at 0 and move left to -3.

To add 6, move right 6 units.  

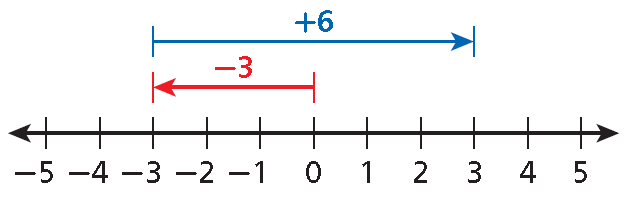
-3 + 6  =  3

Example 2 :

-2 - (-9)

Solution :

On a number line, start at 0 and move left to -2.

To subtract -9, move right 9 units.  

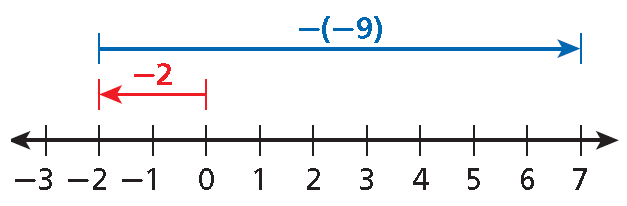
-2 - (-9)  =  7

Absolute Value of a Number

The absolute value of a number is its distance from zero on a number line. The absolute value of 5 is 5. 

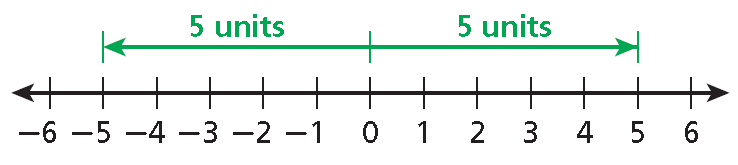
|5|  =  5

|-5|  =  5

Adding Real Numbers

Adding Numbers with the Same Sign : 

Add the absolute values and use the sign of the numbers. 

Adding Numbers with Different Signs : 

Subtract the absolute values and use the sign of the number with the greater absolute value. 

Opposites and Additive Inverses

Two numbers are opposites, if their sum is 0. A number and its opposite are additive inverses and are the same distance from the zero. They have the same absolute value.

For example, 5 and -5 are opposites, because

5 + (-5)  =  0

Additive inverse of 5 is -5 and additive inverse of -5 is 5. 

And also, 5 and -5 have the same absolute value. 

|5|  =  5

|-5|  =  5

Inverse Property of Addition

Words : 

The sum of a real number and its opposite is 0. 

Numbers : 

7 + (-7)  =  (-7) + 7  =  0

Algebra : 

For any real number y, 

y + (-y) + (-y) + y  =  0

Subtracting Real Numbers

Words : 

To subtract a number, add its opposite. Then follow the rules for adding signed numbers.  

Numbers : 

2 - 6  =  2 + (-6)  =  -4

Algebra : 

For two real numbers x and y, 

x - y  =  x + (-y)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.