ADDING AND SUBTRACTING RATIONAL EXPRESSIONS WITH UNLIKE DENOMINATOR
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
There are two methods to add or subtract rational expressions with unlike denominators.
- Least common multiple
- Cross multiplication
Method 1 : (Using Least common multiple)
Step 1 :
If the given two or more rational expressions to added or subtracted with unlike denominators, we will use the Least Common Multiple(LCM).
Step 2 :
To get the result, simplify the numerator and denominator if needed.
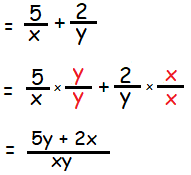
Method 2 : (Using cross multiplication)
Step 1 :
If the given two rational expressions to added or subtracted with unlike denominators, we will use the cross multiplication.
Step 2 :
To get the result, simplify the numerator and denominator if needed.
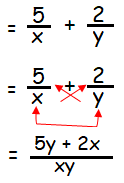
Note :
Sometimes there must be a necessity of using algebraic identities and factorization.
Problem 1 :
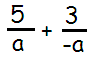
Solution :
The denominators are almost same, using the negative sign in the middle, we get
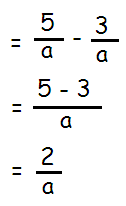
Problem 2 :
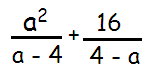
Solution :
(a-4) and (4-a) both are almost same.
By factoring the negative sign from (4-a), we get -(4-a).
= a2/(a - 4) - 42/(a - 4)
= (a2- 42)/(a - 4)
Expanding a2- 42 using the algebraic identity
a2- b2 = (a + b)(a - b)
= (a + 4)(a - 4)/(a - 4)
= a + 4
Problem 3 :
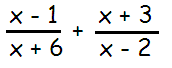
Solution :
Since the denominators are not the same, we are using cross multiplication.
= [(x - 1)(x - 2) + (x + 3)(x + 6)] / (x + 6)(x - 2)
= [(x2 - 2x -1x + 2) + (x2 + 6x + 3x + 18)] / (x + 6)(x - 2)
= [x2 - 3x + 2 + (x2 + 9x + 18] / (x + 6)(x - 2)
= (2x2 + 6x + 20) / (x + 6)(x - 2)
= 2(x2 + 3x + 10) / (x + 6)(x - 2)
= 2(x2 + 3x + 10) / (x + 6)(x - 2)
Problem 4 :
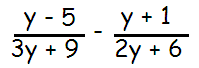
Solution :
Factoring 3 from the denominator of the first fraction and factoring 2 from the denominator of the second fraction, we get
= (y - 5) / 3(y + 3) - (y + 1) / 2(y + 3)
= [2(y - 5) - 3(y + 1)] / 6(y + 3)
= (2y - 10 - 3y - 3) / 6(y + 3)
= (-y - 13) / 6(y + 3)
= -(y + 13) / 6(y + 3)
Problem 5 :
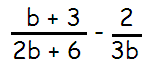
Solution :
Since the denominators are not the same, we are taking the common factor of 2b + 6, we get
= [(b + 3) /2 (b + 3)] - 2/3b
= 1/2 - 2/3b
= (3b - 4)/6b
Problem 6 :
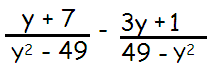
Solution :
Factoring negative from the denominator of the second fraction, we get
= (y + 7)/(y2 - 49) + (3y + 1)/(y2 - 49)
= [(y + 7) + (3y + 1)]/(y2 - 49)
= (4y + 8)/(y2 - 49)
Factoring 2 from the numerator and using algebraic identity (a2 - b2) = (a + b)(a - b)
= 4(y + 2)/(y + 7)(y - 7)
Problem 7 :
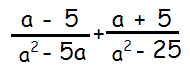
Solution :
= (a - 5) / a(a - 5) + (a + 5) / (a2 - 52)
= [(a - 5) / a(a - 5)] + [(a + 5) / (a + 5)(a - 5)]
= [(a - 5)(a + 5) + a(a + 5)] / a(a - 5)(a + 5)
= [a2 -5a + 5a - 25 + a2 + 5a] / a(a - 5)(a + 5)
= [2a2 + 5a - 25] / a(a - 5)(a + 5)
= [2a2 + 5a - 25] / a(a - 5)(a + 5)
= (a + 5)(2a - 5) / a(a - 5)(a + 5)
= (2a - 5) / a(a - 5)
Problem 8 :
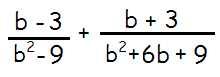
Solution :
= [(b - 3) / (b2 - 32)] + [(b + 3) / (b + 3)(b + 3)]
= [(b - 3) / (b + 3)(b - 3)] + [(b + 3) / (b + 3)(b + 3)]
= 1/(b + 3) + 1/(b + 3)
= (1 + 1)/(b + 3)
= 2/(b + 3)
Problem 9 :
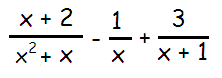
Solution :
Since the denominators are not the same, we are using the least common multiple.
= [(x + 2)/x(x + 1)] - (1/x) + 3/(x + 1)
LCM = x(x + 1)
= [x + 2 - (x + 1) + 3x] / x(x + 1)
= [x + 2 - x + 1 + 3x] / x(x + 1)
= (3x + 3) / x(x + 1)
= 3(x + 1)/x(x + 1)
Cancelling the common factor, we get
= 3/x
Problem 10 :
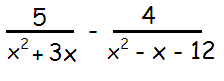
Solution :
By factoring the denominators, we get
x2 + 3x = x (x + 3)
x2 - x - 12 = (x - 4)(x + 3)
= [5/x(x + 3)] - 4/(x - 4)(x + 3)
LCM = x(x + 3)(x - 4)
= [5(x - 4) - 4x]/x(x + 3)(x - 4)
= [5x - 20 - 4x]/x(x + 3)(x - 4)
= (x - 20)/x(x + 3)(x - 4)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
