ADDING AND SUBTRACTING POLYNOMIALS

Adding Polynomials

Polynomials can be added in either vertical form or horizontal form. 

Consider the addition of two polynomials : 

(5x² + 4x + 1) + (2x² + 5x + 2)

In vertical form, align the like terms and add as shown below.   

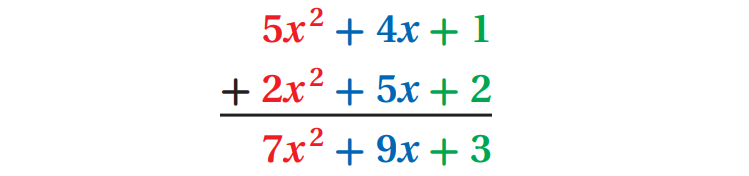
In horizontal form, you use the Associative and Commutative Properties to regroup like terms together and combine them as shown below.  

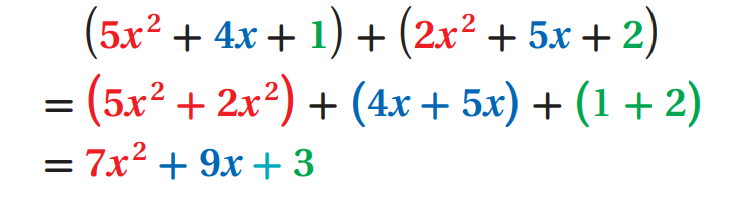
Subtracting Polynomials

To subtract polynomials, remember that subtracting is the same as adding the opposite. To find the opposite of a polynomial, you must write the opposite of each term in the polynomial : 

-(3x² - 5x + 8)  =  -3x² + 5x - 8

Solved Problems

Problem 1 : 

Add :

(2y² - y) + (y² + 3y - 1)

Solution : 

=  (2y² - y) + (y² + 3y - 1)

Group like terms together. 

=  (2y² + y²) + (-y + 3y) - 1

Combine like terms. 

=  3y² + 2y - 1

Problem 2 : 

Add :

(20.2x² + 6x + 5) + (1.7x² - 3x - 8)

Solution : 

=  (20.2x² + 6x + 5) + (1.7x² - 3x - 8)

Group like terms together. 

=  (20.2x² + 1.7x²) + (6x - 3x) + (5 - 8)

Combine like terms. 

=  21.9x² + 3x - 3

Problem 3 : 

The length of a rectangle is represented by 5a + 4b, and its width is represented by 6a - 3b. Write a polynomial for the perimeter of the rectangle. 

Solution : 

Perimeter of the rectangle : 

=  2(length + width)

=  2[(5a + 4b) + (6a - 3b)]

Group like terms. 

=  2[(5a + 6a) + (4b - 3b)]

Combine like terms. 

=  2(11a + b)

Distributive Property. 

=  22a + 2b

Problem 4 : 

Subtract :

(2x² + 6x) - (4x²)

Solution : 

=  (2x² + 6x) - (4x²)

Rewrite subtraction as addition of the opposite. 

=  (2x² + 6x) + (-4x²)

Group like terms together. 

=  (2x² - 4x²) + 6x

Combine like terms. 

=  -2x² + 6x

Problem 5 : 

Subtract :

(k⁴ - 2k) - (3k⁴ - 3k + 1)

Solution : 

=  (k⁴ - 2k) - (3k⁴ - 3k + 1)

Rewrite subtraction as addition of the opposite. 

=  (k⁴ - 2k) + (-3k⁴ + 3k - 1)

Group like terms together. 

=  (k⁴ - 3k⁴) + (-2k + 3k) - 1

Combine like terms. 

=  -3k⁴ + k - 1

Problem 6 : 

The measurements of a photo shown and its frame are shown in the diagram. Write a polynomial that represents the width of the photo.  

Solution : 

Width of the photo : 

=  (6w² + 8) - 2(w² - 3w + 2)

Distributive Property. 

=  6w² + 8 - 2w² + 6w - 4

Group like terms together. 

=  (6w² - 2w²) + 6w + (8 - 4)

Combine like terms. 

=  4w² + 6w + 4

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.