ADDING AND SUBTRACTING DECIMALS WORD PROBLEMS

Problem 1 :

A jar contains 7.5 liters of milk. Lily adds 25.8 grams of sugar and 3.4 liters of water. How much liquid is in the jar?

Solution :

Amount of liquid in the jar :

= 7.5 + 3.4

= 10.9 liters

Problem 2 :

James has $25.65, Charles has $12.75A and Kristen has 19.78. How much money do they all have together?

Solution :

Amount of money that James, Charles and Kristen have together :

= 26.65 + 12.75 + 19.78

= $59.18

Problem 3 :

A bag contains 22.75 cups of sugar. If 2.95 cups of sugar is used for making cookies, find the amount of sugar will be left in the bag.

Solution :

Amount of sugar will be left in the bag after using 2.95 cups of sugar for making cookies :

= 22.75 - 2.95

= 19.8 cups

Problem 4 :

Olivia had $25.55 and Jessica had $23.75. They planned to spend the money together and bought candies for $8.75. How much money did they have after having bought candies?

Solution :

Amount of money that Olivia and Jessica had together after having bought candies :

= 25.55 + 23.75 - 8.75

= 49.30 - 8.75

= $40.55

Problem 5 :

Add the following two decimal numbers with the given conditions.

2.a9 + 3.5b

Conditions :

(i) a + b = 7

(ii) a and b are positive integers and a is an even prime number.

Solution :

It is given that a is an even prime number. We know that 2 is the only even prime number and also it is a positive integer.

a = 2

It is given that a + b = 7.

a + b = 7

2 + b = 7

Subtract 2 from both sides.

b = 5

Since 5 is a positive integer, 5 can be accepted as a value for b.

2.a9 + 3.5b :

= 2.29 + 3.55

= 5.84

Problem 6 :

Evaluate the following expression with the given conditions.

5.7a - 2.b4

Conditions :

(i) a = 3

(ii) b is two times of a.

Solution :

It is given that a = 3 and b is two times of a.

b = 2 ⋅ a

b = 2 ⋅ 3

b = 6

5.7a - 2.b4 :

= 5.73 - 2.64

= 3.09

Problem 7 :

Find the value k in the equation given below.

2.7k + 3.21 = 5.93

Solution :

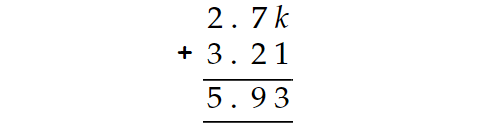
From the above addition two decimal numbers, it is clear that

k + 1 = 3

Subtract 1 from both sides.

k = 2

Problem 8 :

Find the values of x and y in the equation given below.

3.5x + y.78 = 5.32

Solution :

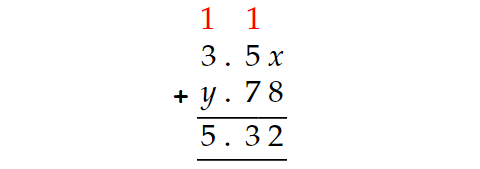
From the above addition decimal numbers,

x + 8 = 12 or 22 or 32.....

If x + 8 = 22 or 32, x has to be a two-digit number. But, it's not possible. So x + 8 must be equal to 12.

Problem 9 :

Find the value of y in the equation given below.

3.74 - 1.3y = 2.38

Solution :

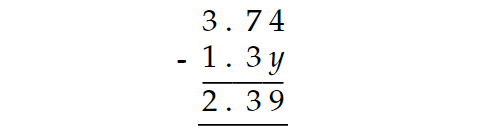
From the initial investigation, we get

4 - y = 9

But, the equation above may be wrong. Because, any positive single digit number y subtracted from 4 will never yield the result 9. And also, the difference between the digits 7 and 3 at tenths place is 3 in the result. Actual difference between 7 and 3 is 4. 

From this, we may guess that 1 would have been borrowed from the digit 7 at tenths place to the digit 4 at hundredths place.

Then the above subtraction as follows.

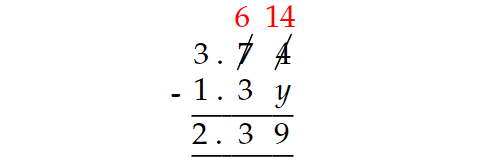
Therefore,

14 - y = 9

Subtract 14 from both sides.

-y = -5

Multiply both sides by -1.

y = 5

Problem 10 :

P, Q and R are three places located on a straight line as shown below.

The distance between the places P and Q is 438.68 miles and that of P and R is 809.95 miles. Find the distance between the places Q and R.

Solution :

Distance between the places Q and R :

QR = PR - PQ

QR = 809.95 - 438.68

QR = 371.27 miles

Problem 11 :

Find the sum of two decimal numbers a.b and b.a, given

a + b = 8

a - b = 3

Solution :

a + b = 8 ----(1)

a - b = 2 ----(2)

(1) + (2) :

2a = 10

a = 5

Substitute a = 5 in (1).

5 + b = 8

b = 3

a.b + b.a :

= 5.3 + 3.5

= 8.8

Problem 12 :

x and y are prime numbers such that

x < 10, y < 10, x > y

If x and y add up to 12, evaluate the following expression. 

3.8x - 2.yy

Solution :

Given : x and y add up to 12.

x + y = 12

List out the prime numbers less than 10.

2, 3, 5, 7

Among the above prime numbers less than 10, two numbers satisfy the equation x + y = 12 are 5 and 7.

Since x > y,

x = 7 and y = 5

3.8x - 2.yy :

= 3.87 - 2.55

= 1.32

Practice Questions

Click here to get detailed answers for the above questions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.