ADD POLYNOMIALS TO FIND PERIMETER

Perimeter : 

Perimeter is the distance around a two-dimensional shape such as square or rectangle or triangle.

If the length of each side of a polygon is polynomial, then we have to add the polynomials to find perimeter of the polygon.  

Examples

Example 1 :

Find the perimeter of the triangle shown below. 

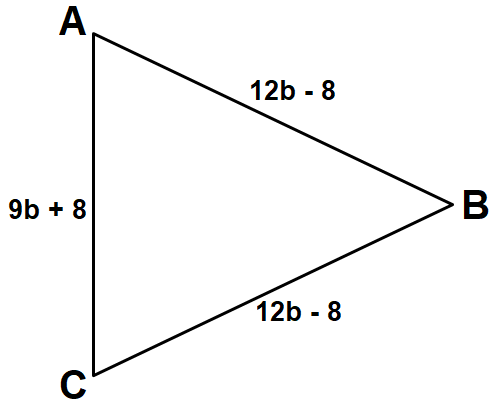
Solution :

Perimeter of triangle ABC is 

=  AB + BC + CA

Substitute. 

=  (12b - 8) + (12b - 8) + (9b + 8)

   =  12b - 8 + 12b - 8 + 9b + 8

   =  (12b + 12b + 9b) + (-8 - 8 + 8)

   =  33b + (-8)

=  33b - 8

Example 2 :

Find the perimeter of the rectangle shown below.

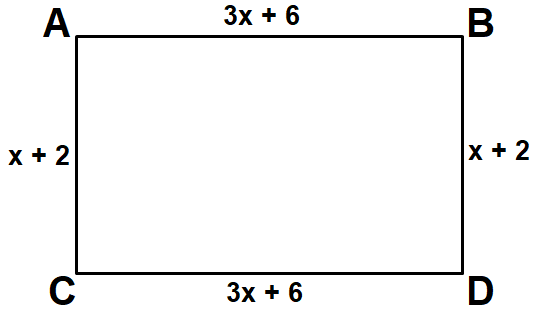
Solution :

Perimeter of rectangle ABCD is

=  AB + BD + DC + CA

Substitute. 

=  (3x + 6) + (x + 2) + (3x + 6) + (x + 2)

=  3x + 6 + x + 2 + 3x + 6 + x + 2

=  (3x + x + 3x + x) + (6 + 2 + 6 + 2)

=  8x + 16

Example 3 :

Find the perimeter of the triangle shown below. 

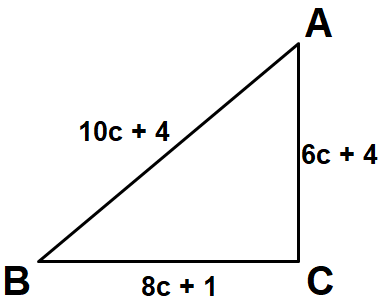
Solution :

Perimeter of triangle ABC is 

=  AB + BC + CA

Substitute. 

=  (10c + 4) + (8c + 1) + (6c + 4)

=  10c + 4 + 8c + 1 + 6c + 4

=  (10c + 8c + 6c) + (4 + 1 + 4)

   =  24c + 9

Example 4 :

Find the perimeter of the triangle shown below. 

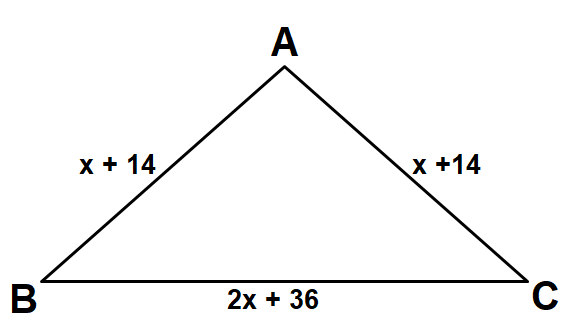
Solution :

Perimeter of triangle ABC is 

=  AB + BC + CA

Substitute. 

=  (x + 14) + (2x + 36) + (x + 14)

=  x + 14 + 2x + 36 + x + 14

=  (x + 2x + x) + (14 + 36 + 14)

=  4x + 64

Example 5 :

Find the perimeter of the rectangle shown below. 

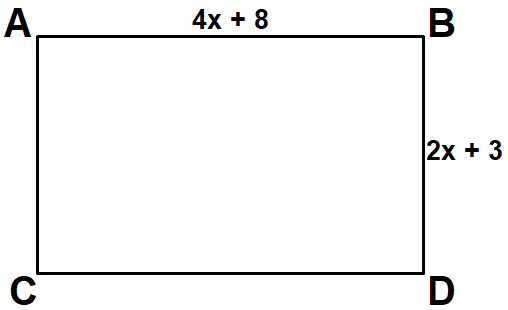
Solution :

In a rectangle, lengths of the opposite sides are equal. 

Then, 

DC  =  AB  =  4x + 8

CA  =  BD  =  2x + 3

Perimeter of rectangle ABCD is

=  AB + BD + DC + CA

=  (4x + 8) + (2x + 3) + (4x + 8) + (2x + 3)

=  4x + 8 + 2x + 3 + 4x + 8 + 2x + 3

=  (4x + 2x + 4x + 2x) + (8 + 3 + 8 + 3)

=  12x + 22

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.