ADD AND SUBTRACT RATIONAL NUMBERS

Addition

Adding Rational Numbers with Same Denominator :

To add two or more rational numbers with same denominator, we have to take the denominator once in common and add the numerators. 

Example :

Simplify : 1/5 + 2/5.

1/5 + 2/5  =  (1 + 2) / 5

1/5 + 2/5  =  3/5

Adding Rational Numbers with Different Denominators :

To add two or more rational numbers with different denominators, we have to follow the steps given below. 

Step 1 : 

Find the least common multiple of the denominators. 

Step 2 : 

Make the denominators same using least common multiple and multiplication. 

Step 3 : 

Take the denominator once in common and add the numerators. 

Example :

Simplify : 1/4 + 1/6.

Least common multiple of (4, 6)  =  12

Multiply the numerator and denominator of the first rational number by 3 to get the denominator 12.

Multiply the numerator and denominator of the second rational number by 2 to get the denominator 12.

1/4 + 1/6  =  (1x3) / (4x3)  +  (1x2) / (6x2)

1/4 + 1/6  =  3/12 + 2/12

1/4 + 1/6  =  (3 + 2) / 12

1/4 + 1/6  =  5/12

Subtraction

Subtracting Rational Numbers with Same Denominator :

To subtract two rational numbers with same denominator, we have to take the denominator once in common and subtract the numerators. 

Example :

Simplify : 2/5 - 1/5.

 2/5 - 1/5  =  (2 - 1) / 5

2/5 - 1/5  =  1/5

Subtracting Rational Numbers with Different Denominators :

To subtract two rational numbers with different denominators, we have to follow the steps given below. 

Step 1 : 

Find the least common multiple of the denominators. 

Step 2 : 

Make the denominators same using least common multiple and multiplication. 

Step 3 : 

Take the denominator once in common and subtract the numerators. 

Example :

Simplify : 1/6 - 1/8.

Least common multiple of (6, 8)  =  24

Multiply the numerator and denominator of the first rational number by 4 to get the denominator 24.

Multiply the numerator and denominator of the second rational number by 3 to get the denominator 24.

1/6 - 1/8  =  (1x4) / (6x4)  +  (1x3) / (8x3)

1/6 - 1/8  =  4/24 - 3/24

1/6 - 1/8  =  (4 - 3) / 24

1/6 - 1/8  =  1/24

Practice Questions

Question 1 :

Simplify the following and write your answer as a proper fraction or as a whole or mixed number.

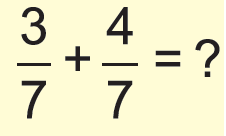
Answer :

Since the denominators are same, we can put only one common denominator and combine the numerators.

  =  (3 + 4)/7 

  =  7/7

  =  1

Question 2 :

Simplify the following and write your answer as a proper fraction or as a whole or mixed number.

Answer :

Since the denominators are same, we can put only one common denominator and combine the numerators.

  =  (12 - 4)/13 

  =  8/13

Question 3 :

Simplify the following and write your answer as a proper fraction or as a whole or mixed number.

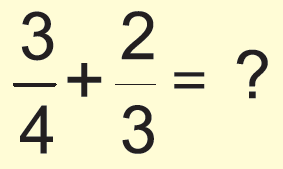
Answer :

Since the denominators are not same, we need to take L.C.M in order to convert the denominators same.

L.C.M (4, 3) = 12

  =  (3/4) x (3/3) + (2/3) x (4/4)

  =  (9/12) + (8/12) 

  =  (9 + 8)/12

  =  17/12

The numerator is grater than the denominator, we have to convert it into mixed fraction. 

=  1 5/12

Question 4 :

Simplify the following and write your answer as a proper fraction or as a whole or mixed number.

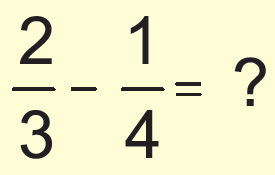
Answer :

Since the denominators are not same, we need to take L.C.M in order to convert the denominators same.

L.C.M (3, 4) = 12

  =  (2/3) x (4/4) - (1/4) x (3/3)

  =  (8/12) - (3/12) 

  =  (8 - 3)/12

  =  5/12

Question 5 :

Simplify the following and write your answer as a proper fraction or as a whole or mixed number.

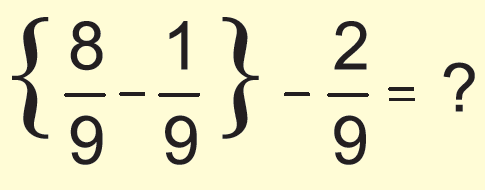
Answer :

Now we need to consider the given question as two parts.

First we have to simplify the fractions inside the parenthesis.

Subtract 2/9 from the simplified answer.

  =  {(8/9) - (1/9)} - (2/9)

  =  (8- 1)/9 - (2/9) 

  =  (7/9) - (2/9)

  =  (7 - 2)/9

=  5/9

Question 6 :

Simplify the following and write your answer as a proper fraction or as a whole or mixed number.

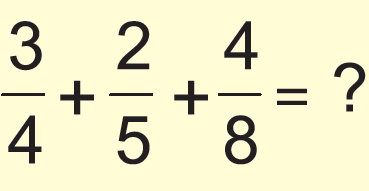
Answer :

Since the denominators are not same, we have to L.C.M in order to convert the denominators same.

L.C.M (4, 5, 8) = 40

  = (3/4) x (10/10) + (2/5) x (8/8) + (4/8) x (5/5) 

  =  (30 + 16 + 20)/40

  =  66/20

  =  33/10

Since the numerator is greater than the denominator, we have to convert into mixed fraction.

=  3 3/10.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.