ADD AND SUBTRACT RADICAL EXPRESSIONS

To add and subtract radicals, we need to be aware of like and unlike radicals.

Like Radicals :

The radicals which are having same number inside the root and same index is called like radicals.

Unlike Radicals :

Unlike radicals don't have same number inside the radical sign or index may not be same.

We can add and subtract like radicals only.

Simplify the following radical expressions :

Example 1 :

√3 + √12

Solution :

= √3 + √12

= √3 + √(2 ⋅ 2 ⋅ 3)

= √3 + 2√3

= 3√3

Example 2 :

√75 + √25

Solution :

= √75 + √3

= √(5 ⋅ 5 ⋅ 3) + √3

= 5√3 + √3

= 6√3 

Example 3 :

√18 + √98

Solution :

= √18 + √98

= √(3 ⋅ 3 ⋅ 2) + √(7 ⋅ 7 ⋅ 2)

= 3√2 + 7√2

= 10√2

Example 4 :

√5 + 2√5 - 5√5

Solution :

= √5 + √20 - √125

= √5 + √(2 ⋅ 2 ⋅ 5) - √(5 ⋅ 5 ⋅ 5)

= √5 + 2√5 - 5√5

= -2√5

Example 5 :

√5 + 3√7 - 4√5 - 5√7

Solution :

√5 + 3√7 - 4√5 - 5√7

Group the like radicals.

= (√5 - 4√5) + (3√7  - 5√7)

Combine the like radicals.

= (-3√5) + (-2√7)

= -3√5 - 2√7

Example 6 :

3√3 + 4√3 - √2

Solution :

= 3√3 + 4√3 - √2

Group the like radicals.

= (3√3 + 4√3) - √2

Combine the like radicals.

= 7√3 - √2

Example 7 :

2(√5 - √3) + 3(√3 - √5)

Solution :

= 2(√5 - √3) + 3(√3 - √5)

Use Distributive Property.

= 2√5 - 2√3 + 3√3 - 3√5

Group the like radicals.

= (2√5 - 3√5) + (-2√3 + 3√3)

Combine the like radicals.

= -√5 + √3

Example 8 :

√8 + √18

Solution :

= √8 + √18

= √(2 ⋅ 2 ⋅ 2) + √(3 ⋅ 3 ⋅ 2)

= 2√2 + 3√2

 = 5√2

Example 9 :

³√16 + ³√54

Solution :

= ³√16 + ³√54

= ³√(2 ⋅ 2 ⋅ 2 ⋅ 2) + ³√(3 ⋅ 3 ⋅ 3 ⋅ 2)

= 2³√2 + 3³√2

 = 5³√2

Example 10 :

√25 + 5³√64

Solution :

= √25 + 5³√64

= √(5 ⋅ 5) + 5³√(4 ⋅ 4 ⋅ 4)

= 5 + 5(4)

 = 5 + 20

= 25

Example 11 :

√12w + √27w

Solution :

= √(12w) + √(27w)

= √(2 ⋅ 2 ⋅ 3 ⋅ w) + √(3 ⋅ 3 ⋅ 3 ⋅ w)

= 2√3w + 3√3w

= 5√3w

Example 12 :

√45y³ + √25y³

Solution :

= √45y³ + √25y³

= √(3 ⋅ 3 ⋅ 5 ⋅ y ⋅ y ⋅ y) + √(2 ⋅ 2 ⋅ 5 ⋅ y ⋅ y ⋅ y)

= 3y√5y + 2y√5y

=5y√5y

= 5y√5y

Example 13 :

³√8x³y⁶ + √9x²y⁴

Solution :

= ³√8x³y⁶ + √9x²y⁴

= ³√(2 ⋅ 2 ⋅ 2 ⋅ x ⋅ x ⋅ x ⋅ y² ⋅ y² ⋅ y²) + √(3 ⋅ 3 ⋅ x ⋅ x ⋅ y² ⋅ y²)

= 2xy² + 3xy²

= 5xy²

Example 14 :

√4p²q⁴ - ³√125p³q⁶

Solution :

= √4p²q⁴ - ³√125p³q⁶

= √(2 ⋅ 2 ⋅ p ⋅ p ⋅ q² ⋅ q²) - √(5 ⋅ 5 ⋅ 5 ⋅ p ⋅ p ⋅ p ⋅ q² ⋅ q² ⋅ q²)

= 2pq² - 5pq²

= - 3pq²

Example 15 :

A square has sides each measuring 2√7 feet. Determine the area of the square.

Solution :

Side length of square = 2√7 feet

Area of square = Side x side

= 2√7 x 2√7

= 4 √7 x √7

= 4√(7x 7)

= 4 (7)

= 28 square feet

So, area of the square is 28 square feet.

Example 16 :

The period of a pendulum is the time required for it to make one complete swing back and forth. The formula of the period P of the pendulum is P = 2 π√(l/32), where l is the length of the pendulum in feet. If a pendulum in a clock tower is 8 feet long, find the period. Use 3.14 for  π.

Solution :

P = 2 π√(l/32)

Here l = 8 feet

P =  2 x 3.14√(8/32)

=  2 x 3.14√(1/4)

=  2 x 3.14 √(1/2 x 2)

= 2 x 3.14 x 1/2

= 3.14 feet

So, the length of period is 3.14 feet.

Example 17 :

A rectangle has width 3√5 centimeters and length 4√10 centimeters. Find the area of the rectangle.

Solution :

Length = 4√10 cm

Width = 3√5 cm

Area of rectangle = length x width

= 4√10 x 3√5

= (4 x 3) √10 √5

= 12 √(5 x 2 x 5)

= 12 x 5√2

= 60 √2 cm²

Example 18 :

A rectangle has length √(a/8) meters and width √(a/2) meters. What is the area of the rectangle ?

Solution :

Length = √(a/8) meters

Width = √(a/2) meters

Area of rectangle = length x width

= √(a/8) x √(a/2)

= √(a/8) x (a/2)

= √(a x a) /(2 x 2 x 2 x 2)

= a/(2 x 2)

= a/4

So, area of the rectangle is a/4 square meter.

Example 19 :

The formula for the area A of the square with side length s is A = s². Solve this equation for s, find the side length of a square having an area of 72 square units.

Solution :

A = s²

Area of square = 72 square units.

72 = s²

s = √72

s = √(6 x 6 x 2)

= 6 √2

So, the side length of the square is 6 √2 units.

Example 20 :

Find the area of the rectangle 

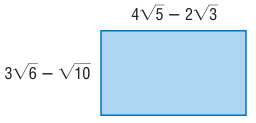
Solution :

Length = 4√5 - 2√3

Width = 3√6 - √10

Area of rectangle = length x width

= (4√5 - 2√3)(3√6 - √10)

= 4√5 (3√6) - 4√5(√10) - 2√3(3√6) - 2√3(√10)

= 12√30 - 4√(5 x 5 x 2) - 6√(3 x 3 x 2) - 2√30

= 12√30 - (4 x 5)√2 - (6 x 3)√2 - 2√30

= 12√30 - 20√2 - 18√2 - 2√30

= 18√30 - 38√2

So, the area of the rectangle is 18√30 - 38√2 square units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.