ADD AND SUBTRACT FRACTIONS

Example 1 :

Find the value of :

3/4 + 1/4

Solution :

The fractions above have the same denominator, that is 4.

So, take the denominator once and combine the numerators.

3/4 + 1/4 = (3 + 1)/4

= 4/4

= 1

Example 2 :

Find the value of :

7/15 + 13/15 + 11/15

Solution :

The fractions above have the same denominator, that is 15.

So, take the denominator once and simplify the numerators.

7/15 + 13/15 + 11/15 = (7 + 13 + 11)/15

= 31/15

Example 3 :

Find the value of :

10/21 - 3/21

Solution :

The fractions above have the same denominator, that is 21.

So, take the denominator once and simplify the numerators.

10/21 - 3/21 = (10 - 3)/21

= 7/21

= 1/3

Example 4 :

Find the value of :

5/28 + 3/28 - 1/28

Solution :

The fractions above have the same denominator, that is 28.

So, take the denominator once and simplify the numerators.

5/28 + 3/28 - 1/28 = (5 + 3 - 1)/28

= 7/28

= 1/4

Example 5 : 

Find the value of :

1/12 + 3/18

Solution :

The fractions above have different denominators.

Find the least common multiple of the denominators.

Least common multiple of (12, 18) = 36.

Now, make the denominator of each fraction 36 using multiplication.

1/12 = (1 ⋅ 3)/(12 ⋅ 3) = 3/36

3/18 = (3 ⋅ 2)/(18 ⋅ 2) = 6/36

1/12 + 3/18 :

= 3/36 + 6/36

= (3 + 6)/36

= 9/36

= 1/4

Example 6 : 

Find the value of :

5/16 - 7/20

Solution :

The fractions above have different denominators.

Find the least common multiple of the denominators.

Least common multiple of (16, 20) = 80.

Now, make the denominator of each fraction as 80 using multiplication.

5/16 = (5 ⋅ 5)/(16 ⋅ 5) = 25/80

7/20 = (7 ⋅ 4)/(20 ⋅ 4) = 28/80

5/16 - 7/20 :

= 25/80 - 28/80

= (25 - 28)/80

= -3/80

Example 7 : 

Ginna’s class measured the lengths of keys. Ginna  displayed the data in a line plot.

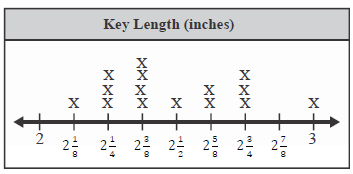
What is the combined length of the shortest key and the longest key? (Add the lengths – not the x’s)

Solution :

Length of shortest key = 2  1/8

Length of longest key = 3

Combined lengths = 2  1/8 + 3

= 5  1/8

Example 8 : 

In a survey on the heaviest zoo animal, 2/8 of Caesar's class voted for rhinoceros and 5/8 voted for elephant. What fraction of the class voted for either a rhinoceros or an elephant as the heaviest animal.

Let x be caesar's class.

Number of Caesar's class voted for rhinoceros = 2x/8

Number of Caesar's class voted for elephant = 5x/8

Fraction of class voted for either a rhinoceros or an elephant = 2x/8 + 5x/8

= 7x/8

Example 9 : 

Find the sum of 1/3 and 2/5

Solution :

To find the sum of 1/3 and 2/5, we have to add these two fractions.

= 1/3 + 2/5

LCM of 3 and 5 = 15

= (1/3) x (5/5) + (2/5) x (3/3)

= 5/15 + 6/15

= (5 + 6)/15

= 11/15

So, the sum of the above fractions is 11/15

Example 9 : 

Find the difference of 1/4 and 2/5

Solution :

To find the difference of 1/3 and 2/5, we have to subtrct these two fractions.

= 1/4 - 2/5

LCM (4, 5) = 20

= (1/4) x (5/5) - (2/5) x (4/4)

= 5/20 - 8/20

= (5 - 8)/20

= -3/20

Example 10 : 

What must 1/5 be increased by to get 2/3 ?

Solution :

Let x be the required fraction.

1/5 + x = 2/3

x = 2/3 - 1/5

x = (2/3) x (5/5) - (1/5) x (3/3)

= 10/15 - (5/15)

= (10 - 5) / 15

= 5/15

= 1/3

So, the required number is 1/3

Example 11 : 

What number is 3/4 less than -1  1/2 ?

Solution :

Let x be the required number.

x - (3/4) = -1  1/2

x - (3/4) = -3/2

Adding 3/4, we get

x = -3/2 + (3/4)

= (-6 + 3)/4

= -3/4

So, the required number is -3/4.

Example 12 : 

Over three successive days Colin builds 1/3, 1/5 and 1/4 of the brickwork of his new garage. What fraction must he complete on the fourth and final day?

Solution :

Quantity of work done by Colin

1/3, 1/5 and 1/4

Amount of work to be completed yet 

= 1 - (1/3 + 1/5 + 1/4)

LCM of 3, 4 and 5 is 60

= 1 - (20 + 12 + 15) / 60

= 1 - 47/60

= (60 - 47)/60

= 13/60

So, on the fourth day, he has to complete 13/60 portion of work.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.