SHSAT PRACTICE QUESTIONS ONLINE FREE

Question 1 :

4/9 is the square root of what number ?

Solution :

From the given option, by taking square of 16/81 we get 4/9.

Hence the answer is 16/81.

Question 2 :

In the following system of equations

3x + 7y = 24, 9x + 4y  =  21 what is (x, y)

Solution :

Let us solve the given system of equations by elimination method.

3x + 7y = 24  -----(1) 

9x + 4y  =  21  -----(2) 

(1) ⋅ 4  ==>  12x + 28y  =  96

(2) ⋅ 7  ==>  63x + 28y  =  147

                   (-)    (-)       (-)

                ---------------------

                 -51x  =  -51

                     x  =  1

By applying x = 1 in (1), we get

3(1) + 7y  =  24

3 + 7y  =  24

7y  =  24 - 3 

7y  =  21

y  =  3

Hence the solution is (1, 3).

Question 3 :

If the first picture means √abcd, then what is the value of second picture.

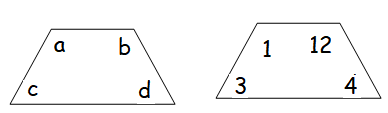
Solution :

√abcd  =  √1(3) (12)(4)  

  =  √144

  =  12

Question 4 :

Which of the following is bigger, the first or second ? Assume X does not equal to Y

First : X/(X - Y)  Second :  Y/(Y-X)

Solution :

To find the which term is greater, we must know the values of X and Y.

Hence the given information is not enough to find answer.

Question 5 :

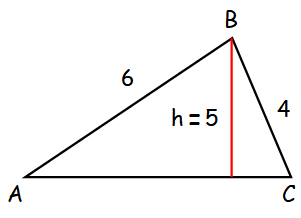
In the figure above, the triangle ABC has an area of 20 square inches, where the height is 5 inches, if the square has the same perimeter as the triangle above, then what is the area of the square ?

Solution :

Area of triangle  =  20

Let "x be the base of the triangle

  (1/2) ⋅ x ⋅ 5  =  20

x  =  20(2/5)

x  =  8 inches.

Perimeter of the triangle  =  AB + BC + CA 

=  6 + 4 + 8

Perimeter of triangle  =  Perimeter of square  =  18

4a  =  18

a  =  18/4  =  9/2

Area of square  =  (4.5)²

=  20.25 square inches.

Question 6 :

The following table shows the class test average score in Ms. Jones Biology class over the years she has been teaching for, what is the median class test score for the years shown ?

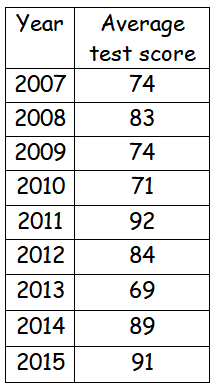
Solution :

69, 71, 74, 74, 83, 84, 89, 91, 92

n = 9 (odd)

Middle term  =  Median  =  83

Hence the Median is 83.

Question 7 :

The wheels of a car have diameter of 10 meters. If the speed of the car is 50 meters per hour, how many revolutions does one wheel make in one hour ?

Solution :

To find the number of revolutions made by the wheel, we have to divide speed of the car by the area covered by 1 revolution.

Area covered in 1 revolution  =  2πr

  =  π(2r)

  =  10 π

Number of revolutions  =  50/10 π

  =  5/π

Question 8 :

A circle is inscribed in a square. What is the probability that a penny, if thrown, will fall in the shaded region below?

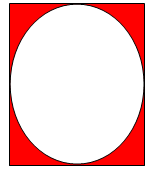
Solution :

Let "r" be the radius of the circle.

2r  =  side length of square

Area of circle  =  πr²

Area of square = a² =  (2r)²  =  4r²

Area of shaded region  =  4r² - πr²

   =  r²(4 - π)

Probability of penny will fall on the shaded region 

=  r²(4 - π)/4r²

=  (4r²/4r²) - πr²/4r²

=  1 - π/4

Question 9 :

What is 10% (10%)/100% ?

Solution :

10% (10%)/100%  =  (10/100)⋅(10/100)/(100/100)

  =  (100/100) / (100/100)

  =  1

Hence the answer is 1.

Question 10 :

The greatest integer function of x, gives the largest integer that is less than x and is represented by ⌊x⌋, what is  ⌊10%⌋ + 1 ?

Solution :

10% means = 10/100  =  0.1

⌊0.1⌋  =  0.0

⌊10%⌋ + 1  =  0 + 1  =  1

Hence the answer is 1.

Question 11 :

Sara is stuck in a circular field. She knows that the area of the circular field is 100 square meters. She walks at a speed of 10 meter per minute. How long will it take her to walk from one end of the circular field to the other end assuming she must cross through the center ?

Solution :

Area of the circular field  =  100 square meter

 πr²  =  100

r²  =  100/π

r  =  √(100/π)  

Diameter of the circular path  =  2√(100/π)  

Time  =  Distance / Speed 

= 2√(100/π) / 10

=  0.2 √(100/π)

Question 12 :

The Fibonacci sequence involves taking two previous numbers and adding them together to get the next. If the first two Fibonacci numbers are 0 and 1, what is the mean of the first 5 Fibonnaci numbers?

Solution :

Required Fibonnaci sequence 

0, 1, 1, 2, 3

Mean  =  (0 + 1 + 1 + 2 + 3)/5

  =  7/5

Question 13 :

If 1 slack  =  x vaks

9 vaks  =  12 hips

How many slack are in 24 hips?

Solution :

x vaks  =  1 slack 

1 vak  =  (1/x) slack  ---(1)

9 vaks  =  12 hips

1 vak  =  (12/9)  hips

1 vak  =  (4/3) hips  ----(2)

(1)  =  (2)

(1/x) slack  =  (4/3) hips

(3/x) slack  =  4 hips

Multiply by 6 on both sides

(18/x) slack  =  24 hips

Question 14 :

What is the value of 11²/10² ?

Solution :

11²  =  11 ⋅ 11  =  121

10² =  10 ⋅ 10  =  100

11²/10²  =  121/100

  =  1.21

Hence the answer is 1.21

Question 15 :

(ab)  =  a + b - b², then what is the value of this expression when a = 5 and b = 2 ?

Solution :

(ab)  =  a + b - b²

  =  5 + 2 - 2²

  =  7 - 4

  =  3

Hence the answer is 3.

Question 16 :

How many non positive integers are between -3 and 5 ?

Solution :

Non positive integers stands for negative integers

-3, -2, -1, 0, 1, 2, 3, 4, 5

The negative integers are -3, -2 and -1.

Hence we have 3 negative integers.

Question 17 :

A number is squared and added to its reciprocal. If that number is represented by x, what is the expression ?

Solution :

"x" be the required number

The sum of square of the number and its reciprocal

  =  x² + (1/x) 

Question 18 :

If I increase the size of a ball by 50% two times in a row, what is the percent increase assuming that the initial size of the ball was 20.

Solution :

Initial size = 20

50% of 20  =  10

New size of ball =  20 + 10  =  30

50% of 30  =  15

New size of ball  =  30 + 15  =  45

Percentage of increase  =  (45 - 30)/30 ⋅ 100%

  =  (15/30) ⋅ 100%

  =  (1/2) ⋅ 100%

  =  50%

Question 19 :

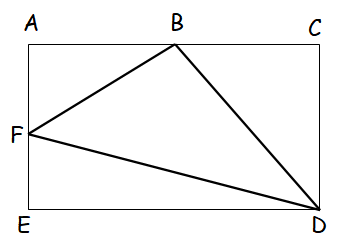
In the figure above, the rectangle ACDE has an area of 440 square meters. the points B and F area the midpoints of the sides AC and AE respectively. What is the area of the triangle BCD?

Solution :

Area of the given rectangle  =  440 square meter 

length ⋅ width  =  440

(l/2) ⋅ width  =  440/2

(l/2) ⋅ width  =  220

BC ⋅ CD  =  220

BC  =  base of the triangle and CD  = height of the triangle

(1/2) BC ⋅ CD  =  (1/2) ⋅ 220

Area of the triangle  =  110

Hence the answer is 110.

Question 20 :

The least common multiple of two numbers, x and y can be represented by LCM  (x,y). The following is true for the concept of the least common multiple :

If we can find integers a and b both x and y respectively such that ax = by = LCM (x, y) then ax or by is the least common multiple of x and y.

What is the least common multiple of √2 ⋅ π ?

Solution : 

Since √2 and π are both irrational, there are no integers, a and b that can satisfy the definition of LCM(x,y).

Hence the LCM does not exist.

(A)  π √2  (B)  2√2π  (C)  2π

(D)  2π²  (E)  Does not exist

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.