PSAT PRACTICE QUESTIONS IN MATH

Question 1 :

If x and y are integers, which is always even ?

(A)  (x + y)/2  (B)  2(x + y)/x  (C)  x - y 

(D)  2(x + y)  (E)  x² + y²

Solution :

Since x and y are integers, the sum of those integers will be odd or even. The multiple of 2 will not be odd. So the answer is 2 (x + y).

Question 2 :

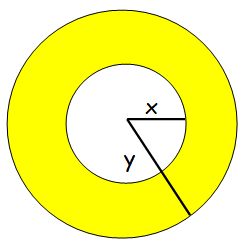
What is the probability that a point chosen will be in the shaded region ?

(A)  y²/x²  (B)  (x + y)²/y²  (C)  x²/(y²-x²)  

(D)  (y²-x²)/y²  (E)  π

Solution :

Sample space  =  n(S)  =  πy²

Let "a" be the event that a point chosen in a shaded region.

Area of shaded region  =  πy² - πx²

n(A)  =  π(y² - x²)

P(A)  =  n (A) / n (S)

  =  π(y² - x²)/πy²

  =  (y² - x²)/y²

Let us look into the next example on "PSAT Practice Questions in Math".

Question 3 :

If q = x + y and x = y + z, what is z in terms of y and q?

(A)  q - 2x  (B)  q - 2y  (C)  2x - q  (D) 2y + q   (E)  2q + x

Solution :

q  =  x + y -----(1)

x  =  y + z  ------(2)

z  =  x - y

From the first equation, let us find the value of x in terms of y and q

x  =  q - y

z  =  (q - y) - y

z  =  q - y - y  

z  =  q - 2y

Question 4 :

What is (5 !)!/ 5! ?

(A)  1  (B)  5  (C)  120  (D)  720  (E)  None of these

Solution :

Let x be 5 !

(5 !)!/ 5!  =  x!/x

  =  x (x- 1)!/x

  =  (x - 1)!

  =  (5! - 1)!

  =  (120 - 1)!

  =  119!

Hence none of the above is the answer.

Question 5 :

What is (a² + 2ab + b²)/(a + b)³ ?

(A)  a + b    (B)  a² + b²    (C)  1/(a + b) 

(D)  1/(a+ b)²    (E)  (a + b)²

Solution :

(a² + 2ab + b²)/(a + b)³

  =  (a + b)²/(a + b)³

  =  1/(a + b)

Question 6 :

It takes 3 cats 3 minutes to catch 3 mice. How many cats are needed to catch 99 mice in 99 minutes ?

(A)  3  (B)  6  (C)  11  (D)  33  (E)  99

Solution :

Given : It takes 3 cats 3 minutes to catch 3 mice.

That is, 

3 cats -----> 3 minutes -----> 3 mice

Let us assume, 

3 cats  =  1 man

Then, we have 

1 man -----> 3 minutes -----> 3 mice

Based on the above statement, we can consider the following situations also. 

1 man -----> 1 minute -----> 1 mouse

1 man -----> 5 minutes -----> 5 mice

1 man -----> 10 minutes -----> 10 mice

In this way, we can have

1 man -----> 99 minutes -----> 99 mice

But, we know that, 

1 man  =  3 cats

Then, we have

3 cats -----> 99 minutes -----> 99 mice

Therefore, 3 cats are needed to catch 99 mice in 99 minutes. 

Question 7 :

The sum of seven consecutive odd integers is 749. What is the largest of the seven integers ?

(A)  99  (B)  103  (C)  11  (D)  113  (E)  115

Solution :

Let x be the odd integer.

6 consecutive odd integers will be (x+2), (x+4), (x+6), (x+8), (x+10) and (x+12).

Sum of seven consecutive integers  =  749

x + x+2 + x+4 + x+6 + x+8 + x+10 + x+12  =  749

7x + 42  =  749

7x  =  749 - 42

7x  =  707

x  =  707/7  ==>  101

Largest number of seven consecutive odd numbers 

  =  x + 12

  =  101 + 12

  =  113

Question 8 :

V = πr²h Using the formula, if r is doubled and h is divided by 2, what is the ratio of the original volume to the new volume ?

(A)  1 : 4  (B)  1 : 2  (C)  1 : 1 (D)  2 : 1  (E)  4 : 1

Solution :

r is doubled means r = 2r

h is divided by 2 means h  =  h/2

New volume :

V₁  =  π(2r)² (h/2)

V₁  =  π(4r²) (h/2)

V₁  =  2πr² h

Ratio of the original volume to the new volume :

  =  V : V₁

  =  πr² h : 2πr² h

  =  1  :  2

Hence the required ratio is 1 : 2.

Question 9 :

A yellow cab has the base fare of $3.50 per ride plus $0.20 for each 1/4 of mile ridden. If a yellow cab costs $ 22.50, how many miles long was the ride ?

(A)  23.75 miles  (B)  42.5 miles  (C)  47.5 miles 

(D)  95 miles  (E)  112.5 miles

Solution :

Let "x" be the number of miles ridden 

To find the (1/4)^th miles of x miles, we have to multiply 4 by x.

So, there are 4x (1/4)^th miles in x miles.

To understand this, let us consider the following example in the picture given below.

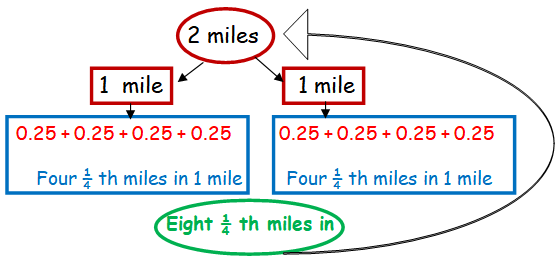
Cost of yellow cab  =  $22.50

3.50 + 0.20 (4x)  =  22.50

0.80x  =  22.50 - 3.50

0.80x  =  19

(80x/100)  =  19

x  =  19(100)/80

x  =  23.75 miles

Hence he traveled 23.75 miles.

Question 10 :

John works 40 hours a week, and his monthly salary in June was $4000. In the month July, John got 4% raise on his monthly salary. In the month of July, what was John's hourly rate ?

(A)  $25  (B)  $26  (C) $40  (D)  $100  (E)  $104

Solution :

June month salary of John  =  $4000

Percentage of salary raised  =  4%

New salary in the month July  =  4000 + 4% of 4000

  =  4000 + 160

  =  4160

John's 1 week salary  =  4160/4  =  1040

He works 40 hours per week.

Hourly rate for the month July  =  1040/40  =  $26

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.