PSAT MATH PRACTICE TEST ONLINE
Question 1 :
It takes George 3 minutes to read 300 words. If each page in a book that he is reading has 750 words, how long will it take George to read 6 pages ?
(A) 30 minutes (B) 45 minutes (C) 60 minutes
(D) 90 minutes (E) 250 minutes
Solution :
Total number of of words in one page = 750
Number of words in 6 pages = 6(750) = 4500
300 words can be read in 3 minutes.
Number of words read in 1 minute = 300/3 = 100
Number of minutes taken to read 4500 words
= 4500/100
= 45 minutes
Question 2 :
[(1/2) - (3/4)]2 + (5/10) =
(A) 9/16 (B) 1/2 (C) 1/16 (D) 3/4 (E) 1/4
Solution :
= [(1/2) - (3/4)]2 + (5/10)
= [(2-3)/4]2 + (5/10)
= (-1/4)2 + (1/2)
= 1/16 + 1/2
= (1 + 8)/ 16
= 9/16
Hence the answer is 9/16.
Question 3 :
If x = 25 ⋅ 32 ⋅ 7, then what is the value of x ?
(A) 1150 (B) 2000 (C) 2015 (D) 2016 (E) 3050
Solution :
x = 25 ⋅ 32 ⋅ 7
x = (32) ⋅ 9 ⋅ 7
x = 2016
Question 4 :
A right cylindrical can is being filled with water. At 1 P.M, it is half full. At 2 P.M, it is 3/4 th full. At this rate, when was it empty ?
(A) 11 : 00 A.M (B) 11 : 30 A.M (C) 12 : 00 P.M
(D) 12 : 30 P.M (E) 3 : 00 P.M
Solution :
From the given information, we know that for every 1 hour 1/4 th of the tank is being filled.
At 1 P.M, 1/2 of the tank is being filled
At 2 P.M, 3/4 of the tank is being filled
At 3 P.M, full tank is being filled
At 12 P.M, 1/4 of the tank is being filled
At 11 A.M, the tank is empty.
Question 5 :
If x8 = (22) 4, what is x2 ?
(A) 2 (B) 4 (C) 8 (D) 64 (E) 128
Solution :
x8 = (22) 4
x8 = 28
Since the powers are equal, we may equate the base.
x = 2
x2 = 22 = 4
Question 6 :
James has a work to finish. He finishes 1/8 of the total work on the first day. What fraction of the work is left ?
(A) 1/8 (B) 3/8 (C) 7/8 (D) 3/4 (E) 1/4
Solution :
Fraction of work left = 1 - (1/8)
= (8 - 1)/8
= 7/8
Question 7 :
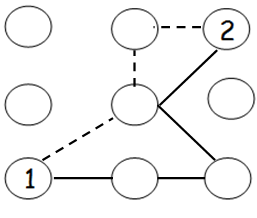
There are two different pathways connecting 1 and and 2. How many fewer steps is the solid line path than the dotted line path. (A step is defined as a line segment connecting 2 circles)
(A) -4 (B) -1 (C) 1 (D) 4 (E) 7
Solution :
Number of steps required to reach from 1 to 2 in solid line = 4
Number of steps required to reach from 1 to 2 in dotted line = 3
= 3 - 4
= -1
Question 8 :
Jackie and Jesse each solve the same problem in a different way
Problem √(a + b) = ?
Jackie's way = √(a + b) = √a + √b
Jesse's way : √(a + b) = √(a+b)
If a = 9 and b = 25, how much bigger is Jakie's way than Jesse's way ?
(A) -2 (B) 0 (C) 2 (D) √36 (E) 8 - √34
Solution :
|
Jackie's way : √(a + b) = √a + √b a = 9 and b = 25 √(a + b) = √9 + √25 = 3 + 5 = 8 |
Jesse's way : √(a + b) = √(a+b) a = 9 and b = 25 √(a + b) = √(a+b) = √(9+25) = √34 |
To find how much bigger is Jakie's way than Jesse's way
= 8 - √34
Question 9 :
If θ { a, b, c, d, e, f, g, h, i } = ab - cd + (ef)2 (gh)2/i
Which cannot be value of θ ?
(A) θ (0, 0, 0, 0, 0, 0, 0, 0, 1)
(B) θ (1, 1, 1, 1, 1, 1, 1, 1, 0)
(C) θ (2, 2, 2, 2, 2, 2, 2, 2, 10)
(D) θ (2,3, 1, 4, 5, 6, 7, 0, 10)
(E) 0
Solution :
The value of θ cannot be ∞, from the given choices, in option B we have 0 for i. By applying this value, we get ∞.
Hence option B is the answer.
Question 10 :
If James grows by 20 inches every day starting Monday. What is the difference in his height between Wednesday and Monday ?
(A) 0 inches (B) 20 inches (C) 30 inches
(D) 40 inches (E) 60 inches
Solution :
Height of James in Monday = 20 inches
in Tuesday = 40 inches
in Wednesday = 60 inches
= 60 - 20
= 40 inches
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Problems Involving Rational Exponents and Radicals
Jun 17, 21 10:07 AM
Problems Involving Rational Exponents and Radicals
-
Factoring 4th Degree Polynomials
Jun 17, 21 08:11 AM
Factoring 4th Degree Polynomials - Concept - Examples with Step by Step Explanation
-
Finding Profit or Loss Percentage Worksheet
Jun 17, 21 05:47 AM
Finding Profit or Loss Percentage Worksheet
