PSAT MATH PRACTICE TEST ANSWERS

Question 1 :

In the figure given below, there is a function plotted and there are 5 points tabeled A through E drawn. For how many points is y(x) equal to 0 ?

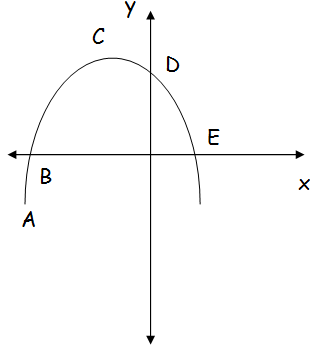
(A)  0  (B)  1  (C)  2  (D)  3  (E)  undefined

Solution :

y(x)  =  0

The graph intersects x-axis at two points. B and E are the roots of the function.

Question 2 :

At what time on a clock will the hands form an acute tangle formed of 60 degree?

(A)  1 : 00 PM  (B)  1 : 15 PM  (C)  2 : 00  PM

(D)  2 : 30 PM  (E)  3 : 00 PM

Solution :

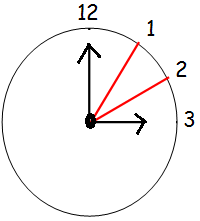
For example, let us consider the picture given above. At 3 PM, it makes an angle 90 degree.

By dividing 90 into three equal parts, we will get each angle as 30 degree.

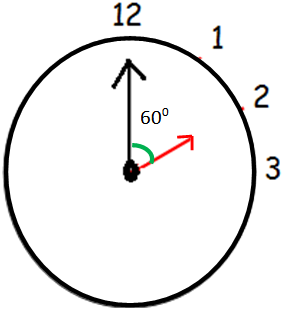
We can see that 2 : 00, 60 degree is formed between the hands 12 and 2.

Question 3 :

A jar contains only red and blue marbles. The probability of picking a red marble is 20% . One blue marble is added to the jar. What is the probability of picking a blue marble ?

(A)  1/3  (B)  1/2  (C)  4/5  (D)  1/6 

(E)  cannot be determined from the information given.

Solution :

Let "A" be the event of getting blue marble

p(A)  =  20/100

P(A)  =  1/5

The answer to this question depends on the number of blue marbles in the bag. Hence the answer is E.

Question 4 :

If a  =  35, what is, (-6)² (-6)(-6) + 6(-6) in terms of a ?

(A)  a + 1  (B)  a²  (C)  a² + 1  (D)  a² + a  (E)  35a

Solution :

=   (-6)² (-6)(-6) + 6(-6)

=  36 (36) - 36

=  36² - 36

=  36(36 - 1)

=  36 (35)

=  (35 + 1) 35

=  (a + 1)a

=  a² + a

Question 5 :

A circle and a regular octagon are having the same perimeter (circumference of the circle). If the side length of the octagon is a, the radius of the circle is r, then what is the radius in terms of the side length of the octagon ?

(A)  4a  (B)  a/π  (C)  4/π  (D)  4a/π  (E)  4π

Solution :

The eight sided polygon is known as octagon.

Circumference of circle  =  Perimeter of octagon

2πr  =  8a

r  =  8a/2π

r  =  4a/π

Question 6 :

What is the least integer greater than the greatest integer less than 1.5 ?

(A)  2  (B)  1.5  (C)  0.5  (D)  1  (E)  0

Solution :

The greatest integer less than 1.5 is 1 and least integer greater than 1 is 2. Hence the answer is 2.

Question 7 :

What is the area of a semicircle in terms of "t" with radius r. "t" is double the value of π

(A)  t² r  (B)  tr² (C)  tr/4  (D)  tr/2  (E)  tr²/4

Solution :

Area of semicircle  =  (1/2)πr²

t  =  2π

π  =  t/2

=  (1/2)(t/2)r²

Area of semicircle  =  (tr²/4)

Question 8 :

If F  =  - kx and greater than 0, then what happens to the vlaue of k if F triples  in value and x remains constant.

(A)  increases  (B)  Doubles  (C)  Decreases  (D)  Remains constant

(E)  cannot be determined from the information given.

Solution :

If F = -kx, then either k or x must be negative. Since F is greater than 0. We do not know which is negative. So, we cannot determine a definite answer.

Hence the answer is E.

Question 9 :

If the length of the side of a square is 7^a, what is the area ?

(A)  7^a  (B)  2 ⋅ 7^a   (C)  49^a  (D)  7^2a  (E)  7a^a

Solution :

Area of square  =  a²

Side of square  =  7^a

  =  (7^a)²

  =  7^2a

Question 10 :

What is the circumference of the dotted section of the circle whose center is O below ?

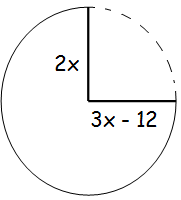
(A)  6π  (B)  12π  (C)  24π  (D)  48π  (E)  64π

Solution :

Equating two radii

3x - 12  =  2x

3x - 2x  =  12

x  =  12

2x  =  24 =  radius

The dotted section is a quadrant. That is, one fourth of the entire circle.

Perimeter of circle  =  2πr

  =  2π(24)

  =  48π

Dividing the circumference by 4, we get 12π. Hence the answer is 12π.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.