IDENTIFY EQUIVALENT RATIOS

Whenever the simplified form of two ratios are equal, then we can say that the ratios are equivalent ratios.

For example, 6 : 4 and 18 : 12 are equivalent ratios, because the simplified form of 6 : 4 is  3 : 2 and the simplified form of 18 : 12 is also 3 : 2. 

We can get equivalent ratios by multiplying or dividing the numerator and denominator by the same number.

Example 1 :

Find the missing numbers. 

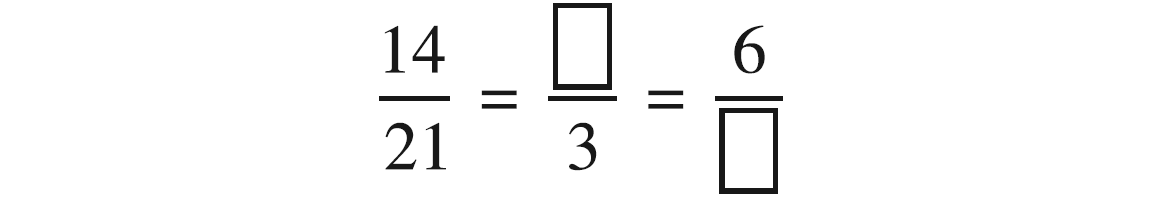
Solution :

It is given that the three ratios are equal.

In order to get the first missing number, we consider the fact that 21 = 3 ⋅ 7. i.e. when we divide 21 by 7 we get 3. This indicates that to get the missing number of second ratio, 14 must also be divided by 7.

When we divide, we have, 14 ÷ 7 = 2

Hence, the second ratio is 2/3

Similarly, to get third ratio we multiply both terms of second ratio by 3.

Hence, the third ratio is 6/9

So, 14/21 = 2/3 = 6/9 [These are all equivalent ratios].

Example 2 :

Find the missing numbers. 

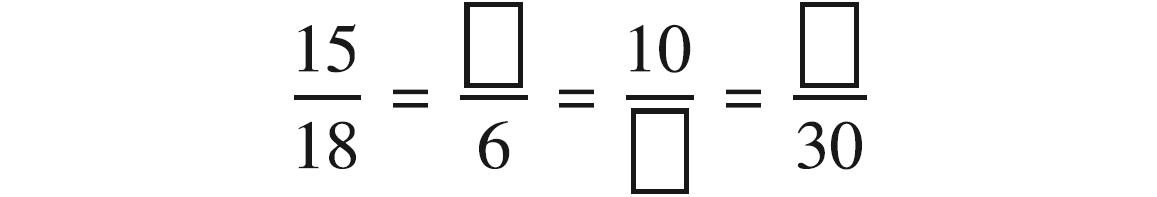
Solution :

(i) In order to get the first missing number, we consider the denominators of first and second fraction.

When we divide 18 by 3, we will get 6, like wise if we divide numerator of first fraction by 3, we will get  5.

The second fraction is 5/6. So the  first missing number is 5.

(ii) Compare 5/6 and 10/?. 

If we multiply the numerator 5 by 2 we will get 10

Like wise, if we multiply the denominator 6 by 2, we will get 12.

The third fraction is 10/12. So the second missing number is 12.

(iii) Compare 10/12 = ?/30.

We cannot say that the number 12 is to be multiplied by which number in order to get 30.

So, let us consider the missing number be x.

10/12 = x/30

Multiply each side by 30. 

(10/12) ⋅ 30 = x

25 = x

The fourth fraction is 25/30. So the third missing number is 25.

Example 3 :

Consider the statement: Ratio of width and length of a hall is 2 : 5. Complete the following table that shows some possible breadths and lengths of the hall.

Solution :

Let x and y be the two unknowns. 

Width and lengths are in the ratio 2 : 5.

If two ratios are equivalent then

 product of means = product of extremes

10 : 25 = x : 50

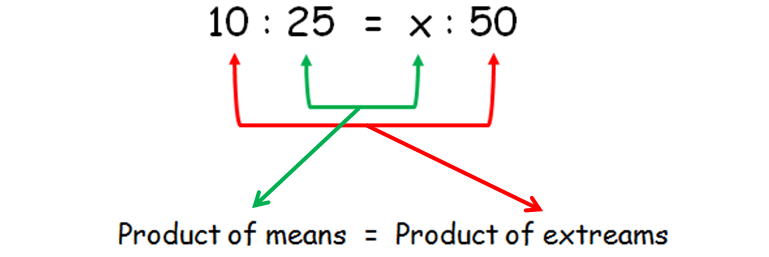
25x = 10(50)

25x = 500

Divide each side by 25.

x = 20

By comparing the first and third columns

product of means = product of extremes

10 : 25 = 40 : x

10x = 40(25)

10x = 1000

Divide each side by 10.

x = 100

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.