HOY AND VUX

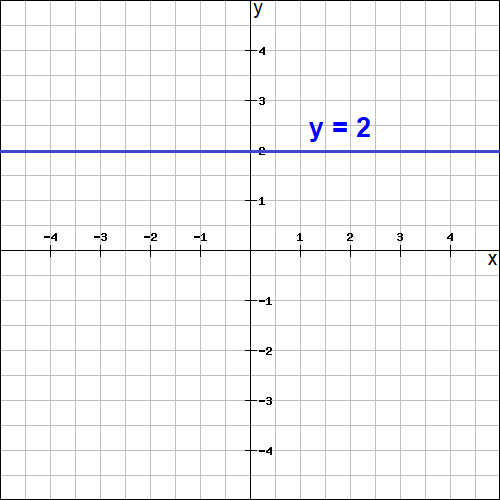
What is horizontal line ?

The line which is parallel to x- axis is known as horizontal line.

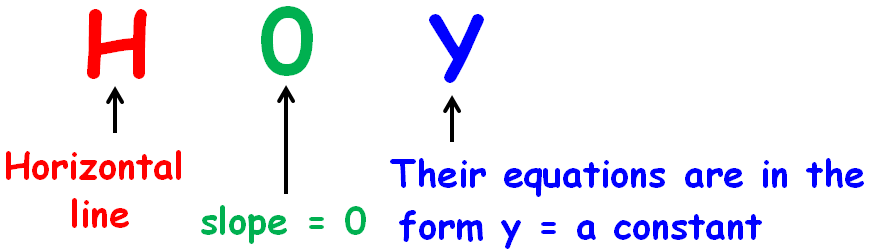
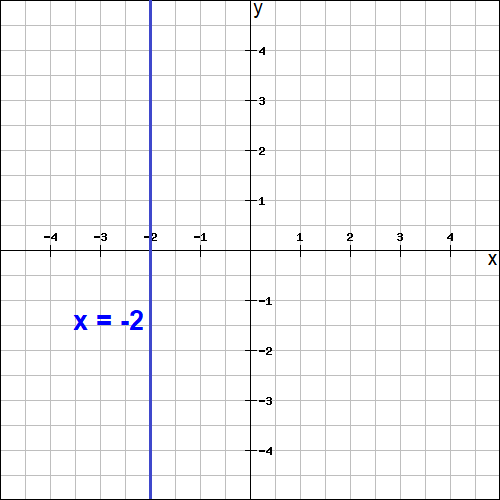
What is vertical line ?

The line which is perpendicular to x-axis is known as vertical line.

What is slope ?

The slope of a line characterizes the direction of a line. To find the slope, you divide the difference of the y-coordinates of 2 points on a line by the difference of the x-coordinates of those same 2 points .

Let us see some examples based on the above concept.

Example 1 :

Find the slope of the line y  =  -3.

Solution :

Because the given line is in the form of x = a constant, it remembers the word (VUX). From this, we can come to know that the given line is vertical line. 

So, its slope is undefined.

Example 2 :

Find the slope of the line x  =  5.

Solution :

Because the given line is in the form of x = a constant, it remembers the word (VUX). From this, we can come to know that the given line is vertical line. 

So, its slope is undefined.

Example 3 :

What is the equation of a line that passes through the point (3, -5) and has an undefined slope ?

Solution :

Because the slope of the line passes which through the point (3, -5) is undefined, the line has to be a vertical line.

This remembers the word "VUX".  

Then, the equation is in the form x  =  a.

'x  =  a' passes through the point (3, -5). 

So, equation of the required line is x = 3.

Example 4 :

What is the equation of the line that has slope=0 and passes through (-2, -5) ?

Solution :

Because the slope of the required line is 0, the line has to be an horizontal line.

This remembers the word "HOY".  

Then, the equation will be in the form of y  =  a.

'y  =  a' passes through the point (-2, -5). 

So, equation of the required line is y  =  -5.

Example 5 :

What is the slope of the line parallel to y  =  -8 ? 

Solution :

y  =  -8 is an horizontal line.

The line which is parallel to y = -8 must also be an horizontal line. 

So, its slope is zero.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.