9th GRADE MATH PRACTICE PROBLEMS

Problem 1 :

Simplify √20 - √225 + √80

Solution :

Decompose 20, 225 and 80 into prime factors.

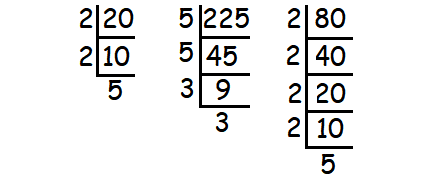
√20  =  √2 ⋅ 2 ⋅ 5  =  2√5

√225  =  √5 ⋅ 5 ⋅ 3 ⋅ 3  =  5 ⋅ 3  =  15

√225  =  √2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5  =  (2 ⋅ 2)√5  =  4√5

Then, we have

√20 - √225 + √80  =  2√5 - 15 + 4√5

√20 - √225 + √80  =  6√5 - 15

√20 - √225 + √80  =  6√5 - 15

√20 - √225 + √80  =  3(2√5 - 5)

Problem 2 :

The perimeter of the rhombus is 20 cm. One of the diagonals is of length 8 cm. Find the length of the other diagonal.

Solution :

In a rhombus, the diagonals are intersecting at right angles.

Perimeter of rhombus  =  20 cm

4a  =  20

a  =  5 cm

Length of diagonal  =  8 cm

Half of diagonal  =  4

Let x be the half of the other diagonal.

5²  =  4² + x²

25  =  16 + x²

x²  =  25 - 16

x²  =  9

x  =  3

Length of other diagonal  =  2(3)

  =  6 cm

Problem 3 :

Jerry and Silvia wanted to go from the southwest corner of a square field to the northeast corner. Jerry walked due east and then due north to reach the goal, but Silvia headed northeast and reached the goal walking in a straight line. How much shorter Silvia's trip was, compared to Jerry's trip? 

Solution :

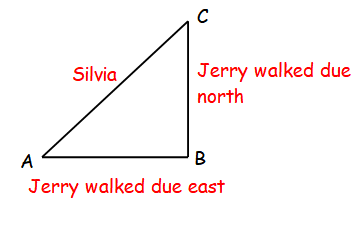
Let AB  =  1, BC  =  1

Then AC  =  √1² + 1²

AC  =  √2

Distance covered by Jerry  =  1 + 1  ==> 2

Distance covered by Silvia  =  √2

Difference of distance covered  =  2 - √2

  =  2 - 1.414

  =  0.586

  =  (0.586/2) ⋅ 100%

  =  30%

So Silvia's trip is 30% shorter than the Jerry's trip.

Problem 4 :

Solve log₁₀ (2x + 50)  =  3

Solution :

log₁₀ (2x + 50) = 3

2x + 50  =  10³

2x  =  1000-50

2x  =  950

x  =  425

So, the value of x is 425.

Problem 5 :

A set has only one element is called ____________ set 

Solution :

A set has only one element is called as singleton set.

Problem 6 :

Which of the following statement represents this Venn diagram?

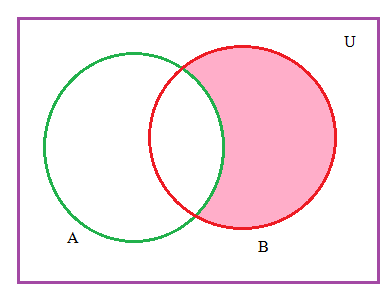
Solution :

In the given venn diagram, the common region for both A and B is not shaded, then the remaining part of B is shaded. So the correct statement is B-A.

Problem 7: 

If (x+p) (x+q) = x²-5x-300, find the value of p² + q²

Solution :

(x+p) (x+q)   =   x²-5x-300

x²+(p+q)x+pq  =  x²-5x-300

p+q  =  -5 and pq  =  -300

p²+q²  =  (p+q)² - 2pq

  =  (-5)²-2(-300)

  =  25 + 600

p²+q²  =   625

Problem 8 :

The point of concurrence of the angle bisector of a triangle is called the _____________ of the triangle.

Solution :

The point of concurrence of the angle bisector of a triangle is called the incenter of the triangle.  9

Problem 9 :

The angles are supplementary and larger angle is twice the smaller angle.Find the angles.

Solution :

Let x be the smaller angle

2x  -  larger angle

2x+x  =  180

3x   180

x  =  60

So, the required angles are 60 and 120.

Problem 10 :

Find the distance between the points

A (-15,-3) and B (7, 1)

Solution :

Distance between two points  =  √(7+15)² + (1+3)²

  =  √(-22)² + 4²

  =  √(484 + 16)

  =  √500

  =  10√5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.