9th GRADE SHSAT PRACTICE TEST WITH SOLUTIONS

To find questions from 1 to 5, please visit the page "SHSAT Math Practice for 9th Graders"

To find questions from 6 to 10, please visit the page "SHSAT Math Test with Answers"

To find questions from 11 to 15, please visit the page "SHSAT Math Test with Solution"

Question 16 :

Maria, Anoki, and Boris are teenagers, and the sum of their ages now is 49.  The sum of their ages 8 years from now will be F, and the sum of their ages 10 years ago was P.  The value of F – P is

(A)  54  (B)  18  (C)  17  (D)  6  (E)  2

Solution :

Sum of ages of Maria, Anoki and Boris  =  49

Sum of their ages 8 years from now  =  49 + 8 + 8 + 8

F  =  73

Sum of their ages 10 years ago  =  49 - 10 - 10 - 10

  =  49 - 30

 P  =  19

F - P  =  73 - 19

=  54

Hence the value of F - P is 54.

Question 17 :

 If (1/4) + (1/x) = 1, then x =

(A)  1/8  (B)  2/3  (C)  4/3  (D)  2  (E)  3

Solution :

(1/4) + (1/x) = 1

(x + 4) / 4x  =  1

x + 4  =  4x 

Subtract x on both sides

-3x + 4  =  0

Subtract 4 on both sides,

-3x  =  -4

x  =  4/3

Hence the value of x is 4/3.

Question 18 :

When the integer N is divided by 7,  the quotient is Q and the remainder is 5.  When N + 24 is divided by 7, the remainder is ‘

(A)  4  (B)  3  (C)  2  (D)  1  (E)  0

Solution :

Let us choose a number which gives the remainder 5 by dividing it by 7.

Let N = 12, by dividing 12 by 7, we get 5 as remainder.

By adding 12 by 24, we get 6. Now let us divide 36 by 7, we get the remainder 1.

Hence 1 is the answer.

Question 19 :

Point B is on line segment AD, and point E is on line segment BC.  The value of x is

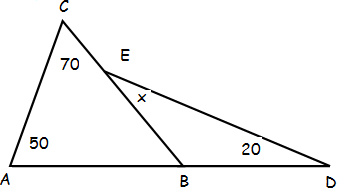
(A)  20  (B)  40  (C)  50  (D)  60  (E)  70

Solution  :

In triangle ABC,

<A + <ABC + <C  =  180

50 + <ABC + 70  =  180

<ABC  =  180 - 120  =  60

In triangle EBD,

<EBD + <BDE + <DEB  =  180

120 + 20 + x  =   180

x  =  180 - 140

 x = 40

Hence the required angle is 40.

Question 20 :

Three-fourths of a number is equal to L.  What is three-halves of that original number, in terms of L?

        (A)  4/3L  (B)  3/2L  (C)  2L  (D)  3L  (E)  4L

Solution :

Let the number be "N"

(3/4) of N  =  L  --(1)

  =  (3/2) of N

Form (1), N = 4L/3

  =  (3/2) (4L/3)

  =  2 L

Hence the answer is 2 L.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.