8th GRADE MATH WORKSHEET WITH ANSWERS

Question 1 :

The quadratic equation n² - 6n - 55 is prime, then the largest value of n is

(A) 12       (B) 15       (C) 28

Solution :

Bye factoring the quadratic equation n² - 6n - 55, we get

  =  (n - 11)(n + 5)

So the largest value of n is 12.

Question 2 :

A rectangle has been divided into congruent squares such that the sum of the perimeters of the squares is numerically equal to the area of the rectangle. What is the length of a side of one of the squares ?

(A) 2         (B) 4        (C) 10

Solution :

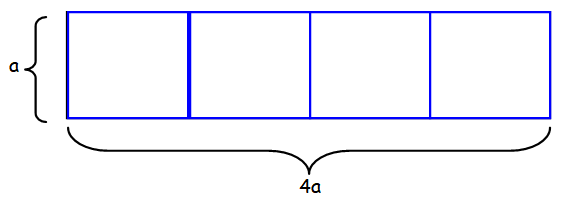
4 ⋅ Perimeter of square  =  Area of rectangle

4(4a)  =  4a(a)

16a  =  4a²

4a  =  16

a  =  16/4

a  =  4

Question 3 :

Paul and Mary are assigned a mathematics project to work on. If Paul works on it alone for 6 hours and let Mary take over, Mary needs another 12 hours to complete.

If Paul works on it for 8 hours then hands it over to Mary, she will need another 6 hours. How many hours does Mary alone to complete the project if Paul has already worked on it for 3 hours ?

(A) 21 hours   (B) 48 hours     (C) 30 hours

Solution :

Let x and y be the number of hours taken by Paul and Mary respectively.

Working rate of Paul  =  1/x

Working rate of Mary  =  1/y

Let 1/x and 1/y as a and b respectively.

Work done by Paul in 6 hours  =  6/x  ==>  6a

Work done by Mary in 12 hours  =  12/y  ==> 12b

6a + 12b  =  1  ------(1)

8a + 6b  =  1  ------(2)

(1)  - (2) ⋅ 2

6a + 12b  =  1

16a + 12b  =  2

(-)     (-)       (-)

--------------------

-10a  =  -1

a  =  1/10 ==> x  =  10

So, Paul is taking 10 days to complete the job.

By applying the value of a in (1), we get

6(1/10) + 12b  =  1

12b  =  1 - (3/5)

12b  =  2/5

b  =  1/30  ==>  y  =  30

Mary is taking 30 days to complete the work.

Working rate of Paul in 1 hour  =  1/10

Work done by Paul in 3 hours  =  3/10

Part of the work to be completed  =  1 - (3/10)

  =  7/10

Time taken by Mary to complete the work 

=  (7/10) / (1/30)

 =  21 hours

Question 4 :

In how many ways can a person go from the origin to the point (3, 3) if he can only move upwards and rightwards and his one step is one unit ?

(A) 10       (B) 20       (C) 30

Solution :

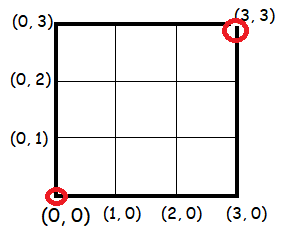
We can reach the point (3, 3) by choosing upwards and right wards directions only.

Choosing any one of the ways, we have to cover 3 horizontal steps and 3 vertical steps.

So, total number of steps is 6.

Number of different ways  =  6!/3!3!

  =  20 ways

Question 5 :

A company could choose any of the three builders (Anthony, Bob and Charles) to build a wall. Anthony would take A days to build the wall. Likewise, Bob and Charles would take B days and C days to build the wall respectively, The table shows the number of days needed to build the same wall if two of them worked together at the same time.

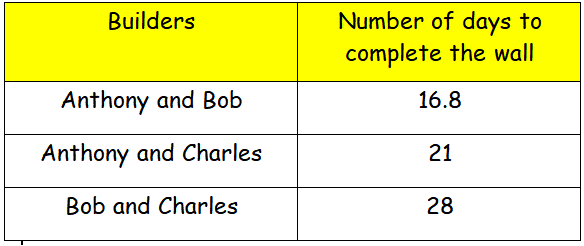
Find the value of A + B + C.

(A)  168      (B) 134        (C) 152

Solution :

Work done by Anthony in 1 day  =  1/A

Work done by Bob in 1 day  =  1/B

Work done by Charles in 1 day  =  1/C

1/A + 1/B  =  1/16.8

1/A + 1/B  =  5/84  ------(1)

1/A + 1/C  =  1/21  ------(2)

1/B + 1/C  =  1/28  ------(3)

(1) - (2)

1/B - 1/C  =  5/84 - 1/21

1/B - 1/C  =  1/84  ----(4)

(3) + (4)

2/B  =  1/28 + 1/84

2/B  =  4/84

2/B  =  1/21

1/B  =  1/42

Applying the value of 1/B in (4), we get

1/42 - 1/C  =  1/84

1/C  =  1/42 - 1/84

1/C  =  1/84

Applying the value of 1/C in (2), we get

1/A + 1/84  =  1/21

1/A  =  1/21 - 1/84

1/A  =  3/84

1/A  =  1/26

The values of A, B and C are 26, 42 and 84 respectively.

A + B + C  =  26 + 42 + 84

A + B + C  =  152

So, the value of A + B + C is 152.

Question 6 :

ABC is a right angled triangle with <CAB  =  90. ADEF is a rectangle such that D lies on AB, E lies on BC and F lies on AC. IF BD  =  4 cm and CF  =  5 cm, find the area in cm² of the rectangle ADEF.

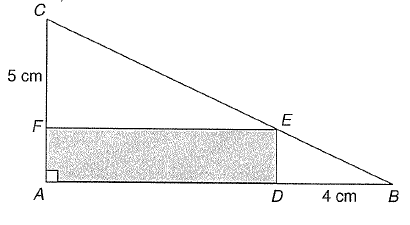
(A)  16 cm²      (B)  20 cm²         (C) 12 cm² 

Solution :

It is not possible to find the length and width of the rectangle. So let us make a reflection 

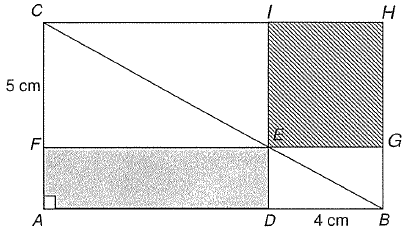
DB  =  EG  =  4 cm and FC  =  IE  =  5 cm

Area of rectangle AFED  =  Area of EGIH

Area of rectangle EGIH  =  length ⋅ Width

  =  4 ⋅ 5

  =  20 cm²

So, area of rectangle AFED is 20 cm².

Question 7 :

Find the total number of prime factors in the product

{(4)¹¹ ⋅ 7⁵ ⋅ (11)² }

(A) 25     (B)  4    (C) 29

Solution :

  =  {(4)¹¹ ⋅ 7⁵ ⋅ (11)² }

  =  {(2²)¹¹ ⋅ 7⁵ ⋅ (11)² }

  =  2²² ⋅ 7⁵ ⋅ 11² 

Total number of factors  =  22 + 5 + 2 

  =  29

So, the total number of factors are 29.

Question 8 :

Rhodes, Watson, Rambo, Peter, Mark and Dwayne are standing in a line with their backs to a wall. How many different orders could they be standing in so that Rhodes and Dwayne are standing next to each other?

(A) 140       (B) 240        (C) 160

Solution :

Considering Rhodes and Dwayne has one unit, the other 4 has separate units.

4 + 1  =  5

  =  5! 2!

  =  120 (2)

  =  240

So, the answer is 240.

Question 9 :

If x  =  5 then find the value of x² - 5

(A) 20      (B) 30      (C) 5

Solution :

By applying x = 5

  =  5² - 5

  =  25 - 5

  =  20

So, the answer is 20.

Question 10 :

A group of seven students working on a project needs to choose two students to present the group's report. How many ways can they choose the two students ?

(A) 30        (B) 21       (C) 38

Solution :

To choose two students out of 7 students, the total number of ways  =  7 C ₂

  =  7!/(7 - 2)! 2!

  =  7!/5!2!

  =  (7 ⋅ 6 ⋅ 5!) / 5! 2!

  =  21 ways

Answer Key

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.