8th GRADE MATH WORKSHEET COMMON CORE

Question 1 :

Four distinct positive whole numbers are arranged in descending order. Given that the sum of the smallest number and the average of the other three is 39, and the sum of the largest number and the average of the other three is 51. What is the largest possible value of the the largest number ?

Solution :

Let a, b, c and d are four distinct numbers in descending order.

a = largest number and d = smallest number

d + (a + b + c)/3  =  39

3d + a + b + c  =  39(3)

3d + a + b + c  =  117  -----(1)

a + (b + c + d)/3  =  51

3a + b + c + d  =  51(3)

3a + b + c + d  =  153 ----(2)

(1) - (2)

2d - 2a  =  117 - 153

2a - 2d  =  36

a - d  =  18

a  =  18 + d

b and c must be greater than d

Let b = d + 1 and c = d + 2

Applying the value of a, b and c in terms of d in (1), we get

3(18 + d) + d + 1 + d + 2 + d  =  117

54 + 3d + 3d + 3  =  117

 3a + 3d  =  117 - 60

 3a + 3d  =  57

a + d  =  19

a  =  19 - d

19 - d < a < 18 + a

If d  =  16, a = 34, b = 17 and c = 18

 So, the four distinct values are 34, 17, 18 and 16.

Question 2 :

In the quadrilateral ABCD below, BE  =  EF  =  FD and CF  =  GF. GFC is a straight line. If the area of the shaded region is 13 cm², find the area of quadrilateral ABCD.

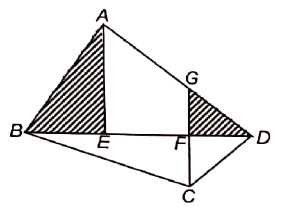
Solution :

BD  =  3 BE

Area of ABD  =  3(Area of ABE)  ----(1)

In triangles GFD and CFD, both are having equal bases and common altitude.

So, Area of GFD  =  Area of ABE

BD  =  3DF

Area of BCD  =  3(Area of CDF) ----(2)

(1) + (2)

Area of ABD+Area of BCD  =  3(Area of ABE + Area of CDF)

Area of ABD  + Area of BCD  =  3 (13)

Area of the quadrilateral  =  39 cm²

Question 3 :

6 identical unit cubes are piled up to build a structure refer to the diagram below on the left for an example. How many structures  area there whose top views are like the diagram below on the right ?

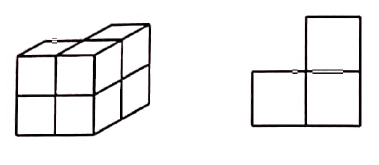
Solution :

Case 1 :

The given  picture in the left hand side is already having 2 cubes in the left hand side, 2 at the center and 2 at the right hand side. (2 - 2 - 2)

Case 2 :

From the bottom layer, we can take the three cubes and arrange them below the left sided cube, so it becomes in the form of 4 - 1 - 1

Like this, we may arrange like 1 - 4 - 1 and 1 - 1 - 4.

Case 3 :

3 cubes in the left hand side, 2 at the center and 1 at the right hand side.(3 - 2 - 1). Similarly (3 - 1 - 2, 2 - 3 - 1, 2 - 1 - 3, 1 - 2 - 3, 1 - 3 - 2).

Possible arrangements are (3 - 2 - 1), (3 - 1 - 2), (2 - 3 - 1), (2 - 1 - 3), (1 - 2 - 3), (1 - 3 - 2), (4 - 1 - 1), (1 - 4 - 1), (1 - 1 - 4) and (2 - 2 - 2).

So there are 10 possible ways.

Question 4 :

In the figure given below, the difference of the areas of the square ABCD and square BEFG is 74 cm². Find the area in cm² of quadrilateral CDGF.

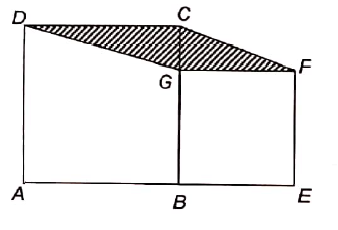
Solution :

Inside the square ABCD, we draw a square BGKI.

Area of BEFG  =  Area of IBGK  =  Area of AIKD  =  74 cm²

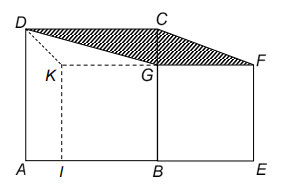
Inside the square ABCD , draw square BGKI which is of same area as square BEFG .

Hence, area of AIKGCD is 74 cm² . Quadrilaterals KDAI and KDCG are of the same area, hence,

Area of KDGC  =  1/2 (area of quadrilateral DAIK)

  =  (1/2) 74

  =  37 cm²

Since the triangles KDG and GCF are of same area, area of quadrilateral CDGF is 37 cm².

Question 5 :

The full score of each common test is 100 marks. Paul has taken common tests and his average score of these 4 tests is 89 marks, if he wants his average score to reach 95 marks or above, at least how many more tests should he take ?

Solution :

The average scored by Paul now  =  89

Need to score the average of 95

The difference between old average and new average

  =  95 - 89

  =  6

Paul needs atleast 6(4)  =  24 marks to get average of 95 marks.

If he is able to score full marks for the subsequent tests, 100 - 95 =  5 marks from each test will contribute to pull up the average score. 

By dividing 24 by 5 we get 4 as quotient and 4 as remainder. So, Paul will take at least 5 more tests.

Question 6 :

There are 10 red marbles, 5 blue marbles and 8 green marbles in a bag. If Janice has only one chance to take marbles out from the bag without looking into the bag, what is the minimum number of marbles she must take out from the bag to ensure she gets at least 2 marbles of the same color ?

Solution :

Case 1 :

If the first two marbles taken out are of same color, then the minimum number of marbles taken out from the bag will be two.

But, it is not sure that the first two marbles taken out from the bag will be same of color. 

So, we neglect this case. 

Case 2 :

If she takes the first marble of one color, second and third marbles of same color or second be one color, first and third of same color, then the minimum number of marbles taken out from the bag will be three.

But, this is also not sure. So, we neglect this case. 

Case 3 :

If she takes first, second and third marbles of different colors, then the fourth marble taken out will be in one of the colors of the first three marbles already taken.

Now, two of the marbles will be of same color. This is possible.

So, Janice must take minimum 4 marbles out from the bag to ensure that she gets at least 2 marbles of the same color. 

Question 7 :

In the game show, a contestant has to answer 8 easy questions correctly to get a silver or 5 difficult questions correctly to get a gold star. Three silver stars can be exchanged to for a gold star at the end of the game. How ever only 30% of the total number of silver can be exchanged for gold stars.Each gold star will win $12 and each silver star will win $3.

Sharon answered 425 easy questions and 42 difficult questions correctly in the game show. What is her maximum winnings ?

Solution :

Number of easy questions answered correctly  =  425

  =  425/8

  =  53

He will get 53 silver coins. 

Number of difficult questions correctly  =  42/5

  =  8

30% of silver coins can be exchanged for gold coin.

30% of 53  =  15

15 coins can be going to be exchanged for gold coins.

3 silver  =  1 gold

15/3  =  5 gold

Total number of gold  =  8 + 5  ==>  13

Total number of silver coins  =  53 - 15  =  38

Amount he can win  =  13(12) + 38(3)

  =  156 + 114

  =  270

Question 8 :

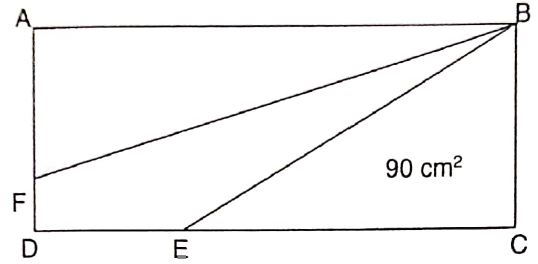
In the figure above shows a rectangle ABC. The ratio of CE : ED is 3 : 2 and the ratio of AF : FD is 7 : 3. The area of the triangle BCE is 90 cm². Find the area of triangle of AFB.

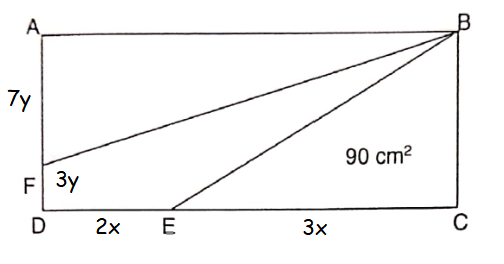
Area of triangle BEC  =  (1/2) ⋅ EC ⋅ BC

90  =  (1/2) ⋅ 3x ⋅ 10y

90  =  15xy

xy  =  90/15

xy  =  6

Area of triangle AFB  =  (1/2) ⋅ AB ⋅ AF

  =  (1/2) ⋅ 5x ⋅ 7y

  =  35xy/2

  =  35(6)/2

  =  105 cm²

Answers

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.