8th GRADE MATH QUIZ QUESTIONS

Question 1 :

Ronald has wondered that who else participates in math team, physics team, and choir. There are 300 people who participate in at least one of the three activities, 150 who participate in choir, 200 who participate in math team, 32 who participate in physics team, 70 who participate in both choir and math team, 12 who participate in both choir and physics team, and 8 who participate in both math team and physics team. How many people participate in all three activities?

(A) 8         (B) 15           (C) 10 

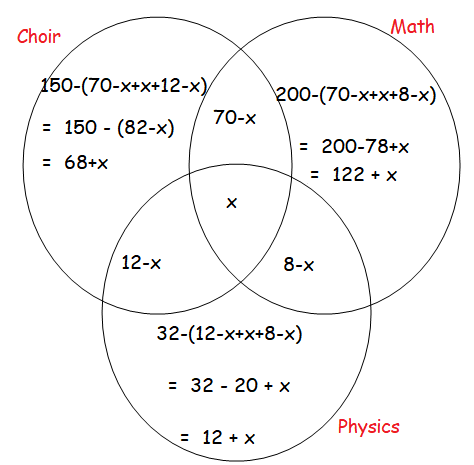
68 + x + 70 - x + 122 + x + x + 12 - x + 8 - x + 12 + x  =  300

 292 + x  =  300

x  =  300 - 292

x  =  8

So, the number of people who participate in all three activities is 8.

Question 2 :

Find the angle formed by a minute hand and hour hand of clock at 7 : 10 pm.

(A) 180         (B) 155           (C) 100 

Solution :

Angle formed when it rotates a complete 12 hours  =  360

Angle between two values  =  360/12

  =  30

Angle between hour hand and minute hand exactly at 7'o clock is 

=  30(5) + 30(10/60)

=  150 + 5

=  155

So, the required angle is 155 degree.

Question 3 :

David and James have a 300-square-foot lawn. It takes David 30 minutes to mow the lawn alone, and it takes James 20 minutes to mow the lawn alone. If David and James work together to mow the lawn at the same time, how long, in minutes, will it take them to mow it?

(A) 13         (B) 12         (C) 11

Solution :

Work done by David in 1 minute  =  1/30

Work done by James in 1 minute  =  1/20

Work done by altogether in 1 minute  =  (1/30) + (1/20)

=  1/12

Time taken by both to complete the work  =  12/1

=  12 days

Question 4 :

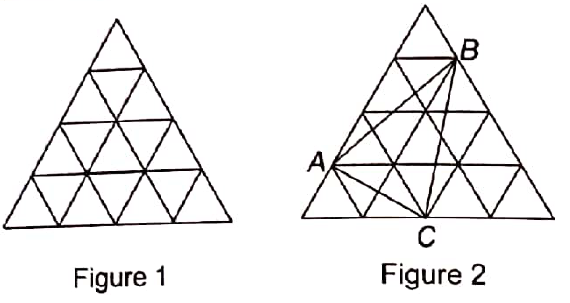
In the figure 1 below, the area of each triangle is 5 cm². Join the three vertices A, B and C to form a triangle shown in figure 2. Find the area (in cm²) of triangle ABC.

Solution :

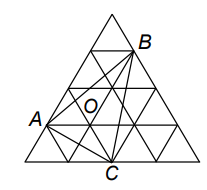
Considering the triangle AOB and BOC, it is clear they  have equal area.

In triangle AOB, there are 4 triangles involving and having half of area of 4 triangles.

Area of AOB  =  (1/2) Area of 4 triangles

Area of 1 triangle  =  5 cm²

Area of AOB  =  (1/2) ⋅ (20)  ==>  10

Area of BOC  =  (1/2) ⋅ (20)  ==>  10

Area of AOC  =  5 cm²

Area of the given triangle  =  10 + 10 + 5

  =  25 cm²

Question 5 :

The current age of two brothers add upto 42. A few years ago, when the elder brother was at the current age of younger brother, the younger brother was exactly half the elder brother's current age. How old is the elder brother now ?

Solution :

Let x and y be the current ages of elder brother and younger brother respectively.

x + y  =  42  ----(1)

Few years ago, age of elder brother  =  x - n

x - n  =  y  ----(2)

y - n  =  x/2  ----(3)

From (2), n  =  y - (x/2) 

x - y + (x/2)  =  y

3x/2  =  2y

3x - 4y  =  0

From (1), y  =  42 - x

3x - 4(42 - x)  =  0

3x - 168 + 4x  =  0

7x  =  168

x  =  168/7

x  =  24

So, his elder brother's current age is 24.

Question 6 :

The 6 digit number 1082ab is a multiple of 12. How many different values of the last 2 digit number ab are there ?

Solution :

If a number is divisible by 12, then it is also divisible by 3 and 4.

Let us divide 1082 by 12

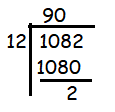
From this, we understood that the remaining part of the given number starts with 2.

By guess,

12 (15)  =  180 (Doesn't start from 2)

12 (17)  =  204 (least number starts with 2 and it is divisible by 12) ...........

12 (24)  =  288 (Largest numbers starts with 2 and it is divisible by 12).

Between 17 to 24 (inclusive), we have 8 values divisible by 12.

Question 7 : 

In a trapezium ABCD below, the area of triangle APB and triangle are 10 cm² and 12 cm² respectively. If AB/CD =  2/3, find the area of (in cm²) of the shaded region.

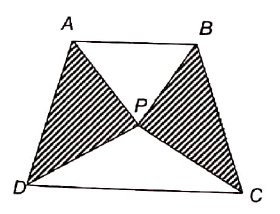
Solution :

From the area of the trapezium, if we subtract the area of unshaded region, we can find the area of shaded region.

Area of triangle ABP  =  (1/2) ⋅ base ⋅ height

AB/CD  =  2/3

Let AB  =  2a and CD  =  3a

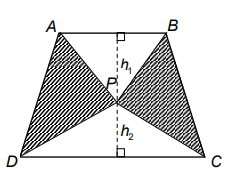
Area of triangle APB  =  (1/2) ⋅ 2a ⋅ h₁

10  =  ah₁

h₁  =  10/a

Area of triangle PDC  =  (1/2) ⋅ 3a ⋅ h₂

12  =  (3a/2) h₂

h₂  =  8/a

Bases of trapezium are 3a and 2a

Height of trapezium  =  (10/a) + (8/a)

  =  18/a

Area of trapezium  =  (1/2) ⋅ height ⋅ (AB + CD)

=  (1/2) ⋅ (18/a) ⋅ (2a + 3a)

=  (1/2) ⋅ (18/a) ⋅ 5a

 =  45 cm²

Area of shaded region  =  45 - 10 - 12

=  23 cm²

Question 8 :

Two distinct numbers from 1 to 100 inclusive will form a pair if the sum of these two is a multiple of 5. How many different pairs are there ?

Solution :

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, .......................

By analyzing the numbers, we can understand the following.

Set A  =  Some of the number are multiple of 5

A  =  {5, 10, 15, 20, ............}

Set B  =  By dividing some of the numbers, we get 1 as remainder.

B  =  {1, 6, 16, 21, 26,..........}

Set C  =  By dividing some of the numbers, we get 2 as remainder.

C  =  {2, 7, 12, 17, 22,..........}

Set D  =  By dividing some of the numbers, we get 3 as remainder.

D  =  {3, 8, 13, 18, ...........}

Set E  =  By dividing some of the numbers, we get 4 as remainder.

E  =  {4, 9, 14, 19,.............}

From 1 to 100, there are 20 numbers as a multiple of 5.

Select two of the numbers from set A

Case 1 :

If we chose the pair from A, we may select

=  (20 ⋅ 19)/2

=  190

Case 2 :

If we choose other pair, we can take one of the number from set B and other from set E.

=  20 ⋅ 20

=  400

Case 3 :

If we choose other pair, we can take one of the number from set C and other from set D.

=  20 ⋅ 20

=  400

Total number of pairs  =  190 + 400 + 400

=  990

Question 9 :

[x] is defined as the largest integer less than or equal to x and {x}  =  x - [x]

For example,

[4.3]  =  4, {4.3}  =  4.3 - [4.3]  =  0.3

[5]  =  5, {5}  =  5 - [5]  =  0

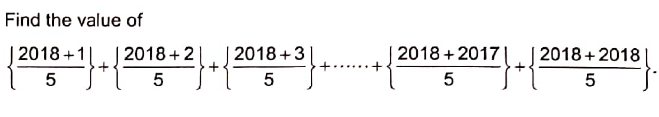
Solution :

(2018 + 1)/5  =  403.8

(2018 + 2)/5  =  404

(2018 + 3)/5  =  404.2

(2018 + 4)/5  =  404.4

(2018 + 4)/5  =  404.6

{403.8}  =  403.8 - 403 ==>  0.8  ==>  4/5

{404}  =  404 - 404 ==>  0

{404.2}  =  404.2 - 404 ==>  0.2  ==>  1/5

{404.4}  =  404.4 - 404 ==>  0.4  ==>  2/5

{404.6}  =  404.6 - 404 ==>  0.6  ==>  3/5

There are 2018 terms like this in the series, so we have 2015/5, that us 403 set of terms.

  =  403[(4/5)+0+(1/5) + (2/5) + (3/5)] + (4/5) + 0 + (1/5)

  =  403(2) + 5/5

  =  806 + 1

  =  807

So, the answer is 807.

Question 10 :

One class of pupils took Math, Science and English tests. 30 pupils passed the Math test, 28 pupils passed the Science test and 25 students passed the English test. If 43 pupils passed at least one test at most how many pupils passed all three tests ?

Solution :

To get the largest possible number of pupils who passed all three tests, the 43 pupils would pass exactly one test or all three tests.

Hence, at most 

  =  (30 + 28 + 25 - 43)/2

  =  20

So, 20 pupils passed all three tests.

Answers

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.