8TH GRADE MATH PROBLEMS WITH ANSWERS

Question 1 :

What is the smallest number by which 256 may be divided so that the quotient is perfect cube? 

(A) 2               (B) 3               (C) 4

Solution :

To find the number required to divide 256 such that the quotient is a perfect cube, we have to decompose 256 into prime factors.  

= ∛256 = ∛(2⋅2⋅2⋅2⋅2⋅2⋅2⋅2) When we group the prime factors inside the cube root as triples, we left over with 2⋅2. That is 4.   Hence 4 is the smallest number required to divide 256 so that the quotient is a perfect cube.

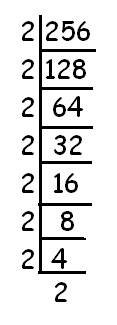Question 2 :

How many digits are there in the square root of 4456321?

(A) 2 digits        (B) 4 digits      (C) 3 digits

Solution :

Square root of 1 digit and 2 digit number contains 1 digit.

Square root of 3 and 4 digit number contains 2 digits.

Square root of 5 and 6 digit number contains 3 digits.

Square root of 7 and 8 digit number contains 4 digits.

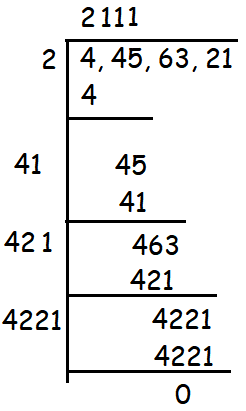
So, the square root of the given number has 4 digits.

Question 3 :

Find the value of 3x³ + 4x² + x - 5 when x = -3.

(A) -53                 (B) -71               (C) -32

Solution :

Let f(x) = 3x³ + 4x² + x - 5.

Substitute x = -3.

f(-3) = 3(-3)³ + 4(-3)² + (-3) - 5

= 3(-27) + 4(9) - 3 - 5

= -81 + 36 - 3 - 5

= -53

Question 4 :

The perimeter of a rectangle is 52 cm. If its width is 2 cm more than one-third of its length, find the dimensions of the rectangle.

(A) 12 cm and 4 cm

(B) 18 cm and 8 cm

(C) 15 cm and 9 cm

Solution :

Perimeter of a rectangle = 52 cm.

2(length + width)  =  52 ==>  l + w  =  26

Let x be the length. The, width = x/3 + 2.

x + (x/3) + 2 = 26

[(3x + x)/3] +2 = 26

4x/3 = 24

4x = 72

x = 18

Width = 18/3 + 2

= 6 + 2

= 8 cm

So, the required dimensions are 18 cm and 8 cm.

Question 5 :

What must be added to each of the numerator and the denominator of the fraction 7/11 to make it equal to 3/4.

(A) 9                    (B) 5             (C) 12

Solution :

Let x be the required number to be added to both numerator and denominator of the fraction.

(7 + x)/(11 + x)  =  3/4

4(7 + x)  =  3(11 + x)

28 + 4x  =  33 + 3x

4x - 3x  =  33 - 28

x  =  5

So, 5 is the required number to be added to make the fraction 7/11 as 3/4.

Question 6 :

A line which intersects two or more lines at a distinct points is called a ____________

(A) concurrent       (B) Intersecting     (C) Transversal

Solution :

A line which intersects two or more lines at a distinct points is called a concurrent.

Question 7 :

The opposite angles of a cyclic quadrilateral are _______________

(A) Supplementary    (B) Complementary (C) None of these

Solution :

The sum of opposite angles of a cyclic quadrilateral is 180 degree.

So, the answer is supplementary.

Question 8 :

In triangle ABC is inscribed in a circle with center O and BC is a diameter, if angle BAC is 50°, find angle ABC.

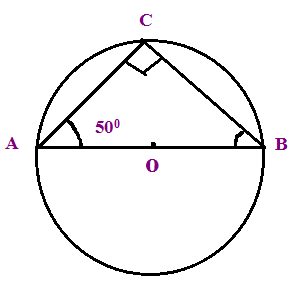
(A)  50°           (B)  40°           (C)  48°

Solution :

In the right triangle ABC,

∠A + ∠B + ∠C  =  180°

50° + ∠B + 90°  =  180°

140° + ∠B  =  180°

∠B  =  40

Question 9 :

The circumference of a circle is 44 cm. Find its area (use π = 22/7) 

(A) 154 cm²      (B) 130 cm²      (C) 145 cm²

Solution :

Circumference of a circle =   44 cm

2πr  =  44

2 ⋅ (22/7) ⋅ r  =  44

r  =  7

Area of circle  =  πr²

  =  (22/7) ⋅ (7)²

  =  154 cm²

Question 10 :

The volume of a right circular cylinder is 1100 cm³ and the radius of its base is 5 cm. Calculate its curved surface area. 

(A) 410 cm²        (B) 125 cm²          (C) 440 cm²

Solution :

Volume of a right circular cylinder  =  1100 cm³

 πr²h =  1100 cm³

Here r = 5

(22/7) ⋅ (5)² ⋅ h  =  1100

h  = 2/7

Curved surface area of cylinder  =  2πrh

  =  2 ⋅ (22/7) ⋅ 5 ⋅ (2/7)

=  440 cm²

So, the curved surface area of cylinder is  440 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.