7 TH GRADE MATH PRACTICE TEST WITH ANSWERS

Question 1 :

If the sum of a number and 4 is 2003, then the number is ?

(A)   1998       (B)  1990        (C)  1999

Solution :

Let x be the required number

x + 4  =  2003

Subtract 4 on both sides

x  =  2003 - 4

x  =  1999

So, the required number is 1999.

Question 2 :

The question paper in an exam consists 80 problems. James has solved 68 of them. The percentage of the problems he has solved?

(A)  50            (B)  80             (C)  85

Solution :

Total number of questions in the question paper  =  80

Number of solved question  =  68

Percentage of problems he has solved  =  (68/80) 100

  =  (17/20) 100

  =  17(5)  =  85

So, 85% of questions solved.

Question 3 :

An author of a math competition was looking through a tentative exam, when he realized that he could not use one of his proposed problems. Frustrated, he had decided to take a nap instead, and slept from 10.47 am to 7.32 pm. For how many minutes did he has sleep ? 

(A)  585     (B)  620     (C)  225

Solution :

To find the number of minutes he has sleep, let us find the number of hours he has slept.

12.00  -  10.47  =  2.13

                            7.32

                          ------

                           9.45  

Number of minutes for 9 hours  =  9 (60)  =  540

      =  540 + 45

      =  585

So, the number of minutes he has sleep 585.

Question 4 :

If a rectangle ABCD has the lengths, AB = 7m and AC = 25, then its area is ?

(A)   130        (B) 150         (C)  168

Solution :

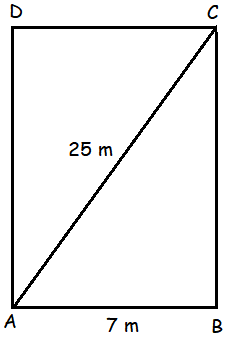
In a right triangle ABC,

AC²  =  AB² + BC²

25²  =  7² + BC²

625 - 49  =  BC²

BC²  =  576

BC  =  √576  =  24

Area of rectangle  =  Length ⋅ Width

  =  7 ⋅ 24

  =  168 m²

So, the area of rectangle 168 m².

Question 5 :

If the diagonal of a square is 4 feet long, then the area of the square is

(A) 5              (B) 9            (C)  8

Solution :

Diagonal of a square  =  4 ft

a² + a²  =  4²

2a²  =  16

a²  =  8

Area of square 8 square feet.

Question 6 :

If two angles are supplementary and one of the angles is 9 times as large as the other, what is the measure of the larger angle?

(A)   162    (B)   150   (C)   165

Solution :

Let "x" be the unknown angle

"9x" be the other angle

x + 9x  =  180

10x  =  180

Divide both sides by 10

x  =  18

9x  =  9(18)  =  162

So, the measure of larger angle is 162.

Question 7 :

ABCD is a square with the length of 8 units each side. A second square A₁B₁C₁D₁ is formed by joining the midpoints of AB, BC, CD,and DA. Find the sum of the areas of these two squares

(A)   96 cm²        (B)  104 cm²        (C)  48 cm²

Solution :

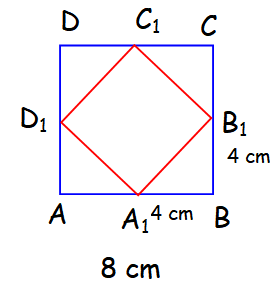
Area of the square ABCD =  a²

  =  8²  =  64 cm²

To find the area of square A₁B₁C₁D₁, we have to find the side length of A₁B₁

  (A₁B₁₎²  =  4² + 4²

  (A₁B₁₎²  =  16 + 16  =  32  =  4√2

Area of square A₁B₁C₁D_{1  =}  (4√2)²   =  32 cm²

Question 8 :

If p + q = 13, q + r = 14, r + p = 15, then the value of r is

(A)   6              (B)   8                 (C)  5

Solution :

p + q = 13  ----(1) 

 q + r = 14  ------(2) 

r + p = 15  ----(3)

(2) - (3)

q + r - r - p  =  14 - 15

q - p = -1  ---(4)

Add 1^st and 4^th equation

p + q + p - q  =  13 + (-1)  =  12

2p  =  12

p  =  6

p + r  =  15

r  =  15 - 6 = 9

So, the value of r is 9.

Question 9 :

The number of three-digit perfect squares are, 

(A)  12          (B)   19             (C)   22

Solution :

The value of 10² is 100,

The value of 18² is 324

The value of 31² is 961.

From 10 to 31, we have 22 numbers.

So, the number of three digit perfect squares are 22.

Question 10 :

A train is running at a speed of 20 m/sec.. If it crosses a pole in 30 seconds, find the length of the train in meters. 

(A)  200 meter       (B)  800 meter       (C)   600 meter

Solution :

The distance covered by the train to cross the pole is

=  Length of the train 

Given : Speed is 20 m/sec and time taken to cross the pole is 30 seconds

We know,  

Distance  =  Speed ⋅ Time 

So,

length of the train  =  Speed ⋅ Time

Length of the train  =  20 ⋅ 30

Length of the train  =  600 meters

So, length of the train is 600 meters.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.