10th GRADE MATH PRACTICE PROBLEMS

Problem 1 :

The sum of an infinite G.P is 4 and the sum of the cubes of the terms is 192. Determine the common ratio.

Solution :

Geometric series :

a, ar, ar², ar³, ..................

Sum of infinite series  =  4

a/(1-r)  =  4 

a³/(1-r)³  =  64

a³/(1-r)(1 - 2r + r²)  =  64----(1)

Sum of cubes of terms of geometric series :

a³, (ar)³, (ar²)³, (ar³)³, ..................

a³, a³r³, a³r⁶, a³r⁹, ..................

Sum of cubes  =  192

a³/(1-r³)  =  192

a³/(1-r)(1+r+r²)  =  192    ----(2)

(1) / (2)

a³/(1-r)(1-2r+r²) / a³/(1-r)(1+r+r²)   =  64/192

(1+r+r²)/(1 - 2r + r²)  =  1/3

(1-2r+r²) / (1+r+r²)  =  3

1-2r+r²  =  3(1+r+r²)

2r² + 5r + 2  =  0

2r² + 4r + r + 2  =  0

2r(r + 2) + 1(r + 2)  =  0

(2r + 1)(r + 2)  =  0

r  =  -1/2 and r  =  -2

The required common ratios are -1/2 and -2.

Problem 2 :

A triangle with sides 3 cm, 4 cm and 5 cm is rotated about the side of length 4 cm. Find the volume of the solid generated.

Solution :

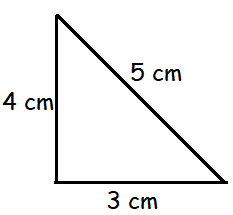
Height of the triangle  =  4 cm and base  =  3 cm

When we rotate the triangle, we will get cone.

Area of the triangle  =  (1/3) ⋅ πr²h

=  (1/3) ⋅ π(3)²4

=  12π

  =  12 cm³

Problem 3 :

If A = {1, 3, 5, 7}, B = {1, 2, 4, 6, 8} and C = {1, 3, 6, 8} then find (A ∪ B) ∩ (A ∪ C).

Solution :

A ∪ B  =  {1, 3, 5, 7} U {1, 2, 4, 6, 8}

A ∪ B  =  {1, 2, 3, 4, 5, 6, 7, 8}

(A ∪ C)  =  {1, 3, 5, 7} U {1, 3, 6, 8}

(A ∪ C)  =  {1, 3, 5, 6, 7, 8}

(A ∪ B) ∩ (A ∪ C)  =  {1, 2, 3, 4, 5, 6, 7, 8}n{1, 3, 5, 6, 7, 8}

(A ∪ B) ∩ (A ∪ C)  =  {1, 3, 5, 6, 7, 8}

Problem 4 :

Let A  =  {0, 1} and B  =  {1, 3} be two sets. Let f: A→B be a function given by f(x) = 2x + 1. Represent this function as a set of ordered pairs.

Solution :

f(x) = 2x + 1

If x  =  0, then f(0)  =  1

If x  =  1, then f(1)  =  3

Required function  =  {(0, 1) (1, 3)}.

Problem 5 :

The sum of three numbers is 24. Among them one number is equal to half of the sum of the other two numbers but four times the difference of them. Find the numbers.

Solution :

Let x, y and z be three numbers.

x + y + z  =  24 -----(1)

x  =  (y + z)/2 

2x - y - z =  0 -----(2)

x  =  4(y - z)

x - 4y + 4z  =  0-----(3)

(1) + (2)

3x  =  24

x  =  8

By applying the value of x in x  =  (y + z)/2, we get

y + z  =  16 ----(4)

By applying the value of x in 4(y - z), we get

y - z  =  2 ----(5)

(4) + (5)

2y  =  18

y  =  9

By applying the value of y in (4), we get

9 + z  =  16

z  =  7

So, the values of x, y and z are 8, 9 and 7 respectively.

Problem 6 :

Find the remainder when 6x⁴ - 11x³ + 5 x² - 7x + 9 is divided by (2x-3).

Solution :

Let p(x)  =  6x⁴ - 11x³ + 5 x² - 7x + 9

2x-3  =  0

x  =  3/2

p(3/2)  =  6(3/2)⁴-11(3/2)³+5(3/2)²-7(3/2)+9

  =  6(81/16)-11(27/8)+5(9/4)-(21/2)+9

  =  243/8 - 297/8 + 45/4 - 21/2 + 9

  =  (243 - 297 + 90 - 84 + 72)/8

  =  24/8

  =  3

So, the remainder is 3.

Problem 7 :

If 2, x, 26 are in arithmetic progression. Find the value of x.

Solution :

If the sequence is in arithmetic progression. then

a₂ - a₁  =  a₂ - a₁

x-2  =  26-x

x + x  =  26+2

2x  =  28

x  =  14

Problem 8 :

Determine the value of m if x+1 is a factor of

x³+mx²+19x+12

Solution :

p(x)  =  x³+mx²+19x+12

x + 1  =  0

x  =  -1

p(-1)  =  (-1)³+m(-1)²+19(-1)+12

-1+m-19+12  =  0

-20+m+12  =  0

-8+m  =  0

m  =  8

Problem 9 :

Find the square root of x² + 10 x + 25 

Solution :

√x² + 10 x + 25  =  √x² + 2⋅x⋅5 + 25

  =  √(x + 5)²

  =  |x+5|

Problem 10 :

The age of the father is square of his daughter Henna. Five years hence the father is three times as old as Henna. Find the present ages of henna.

Solution :

Let x be the age of Henna. 

Age of his father  =  x²

Age after 5 years,

Henna's age  =  x + 5

Father's age  =  x² + 5

x² + 5  =  3(x + 5)

x² -3x+5-15  =  0

x² -3x-10  =  0

(x-5)(x+2)  =  0

x  =  5 and x  =  -2

So, present age of Henna is 5.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.