FIND COEFFICIENT OF VARIATION EXAMPLE PROBLEMS

Formula to calculate coefficient of variation from mean and standard deviation is  

=  (σ/x̄) ⋅ 100%

Here σ is the standard deviation and x̄ is the mean. 

Formula to find standard deviation σ is

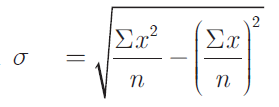
Formula to find arithmetic mean x̄ is

x̄  =  ∑x/n

Example 1 :

If n = 10, x̄ = 12 and Σx² = 1530, then calculate the coefficient of variation.

Solution :

The formula to find coefficient of variation is

C.V  =  (σ/x̄) x 100

σ  =  √(Σx²/n) - (Σ x/n)²

=  √(1530/10) - 12²

=   √153 - 144

=  √9

=  3

Coefficient of variation C.V  =  (σ/x̄) x 100

=  (3/12) x 100

=  (1/4) x 100

=  25

Example 2 :

Calculate the coefficient of variation of the following data

20, 18, 32, 24, 26

Solution :

First let us write the given data in ascending order

20, 18, 32, 24, 26

Coefficient of variation C.V  =  (σ/x̄) x 100

=  (4.9/24) x 100

=   490/24

=   20.416 

=  20.42

Example 3 :

If the coefficient of variation of a collection of data is 57 and its standard deviation is 6.84, then find the mean.

Solution :

Coefficient of variation C.V  =  57

Standard deviation (σ)  =  6.84

(σ/x̄) x 100  =  57

(6.84/x̄) x 100  =  57

x̄  =  684/57

x̄  =  12

Example 4 :

A group of 100 candidates have their average height 163.8 cm with coefficient of variation 3.2. What is the standard deviation of their heights?

Solution :

mean of height of 100 candidates(x̄)  =  163.8

coefficient of variation (C.V)  =  3.2

(σ/x̄) ⋅ 100 = 3.2

(σ/163.8) ⋅ 100 = 3.2

σ  =  (3.2 x 163.8)/100

σ  =  5.2416

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.