10th GRADE MATH PRACTICE QUESTIONS

Problem 1 :

The ratio of incomes of two persons is 9 : 7 and the ratio of their expenditures is 4 : 3. If each of them manages to save $2000 per month, find their monthly incomes.

Solution :

Let 9x, 7x be incomes of two persons.

Let 4y and 3y are expenditure of two persons.

9x - 4y  =  2000 ----(1)

7x - 3y  =  2000 ----(2)

(1) ⋅ 3 ==>    27x - 12y  =  6000

(2) ⋅ 4 ==>  -28x + 12y  =  -8000

(3) - (4)   ------------------------

                   -x  =  -2000

By applying the value of x  =  2000 in (1), we get

9(2000) - 4y  =  2000

4y  =  16000

y  =  4000

9x  =  18000 and 7x  =  14000

So, the incomes of two persons are 18000 and 14000 respectively.

Problem 2 :

Solve the following pair of linear equations by the elimination method 3x + 4y = 10 and 2x – 2y = 2.

Solution :

3x + 4y  =  10 ----(1)

2x – 2y  =  2 ----(2)

                    3x + 4y  =  10

(2) ⋅ 2 ==>    4x - 4y  =  4

                   ----------------

                     x  =  14

By applying the value of x in (2), we get

28 - 2y  =  2

2y  =  26

y  =  13

So, the solution is (14, 13).

Problem 3 :

Two players, Jessy and mark, play a tennis match. It is known that the probability of Jessy winning the match is 0.62. What is the probability of Mark winning the match ?

Solution :

Probability of Jessy is winning the match  =  0.62

Probability of Mark is winning the match  =  1 - 0.62

  =  0.38

Problem 4 :

Two dice, one blue and one red, are thrown at the same time. Write down all the possible outcomes. What will be  the probability that the sum of the two numbers appearing on the top of the dice is 8?

Solution :

Sample space  =  

{(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) 6 (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) }

n(s)  =  36

Let A be the event of sum as 8.

A  =  {(2, 6) (3, 5) (4, 4) (5, 3) (6, 2)} 

n(A)  =  5

p(A)  =  n(A)/n(S)

p(A)  =  5/36

Problem 5 :

James buys a fish from a shop for his aquarium. The salesman takes out one fish at random from a tank containing 5 male fish and 8 female fish. What will be the probability that the fish taken out would be  male fish?

Solution :

Sample space  =  Total number of fishes

n(S)  =  5 male + 8 female

n(S)  =  13 fishes

Let A be the event of getting male fish.

n(A)  =  5

p(A)  =  n(A)/n(S)

p(A)  =  5/13

So, the probability of getting male fish is 5/13.

Problem 6 :

If the points A (6, 1), B (8, 2), C (9, 4) and D (t, 3) are the vertices of a parallelogram, taken in order, find the value of t.

Solution :

Midpoint of diagonal AC  =  Midpoint of diagonal BD

Midpoint  =  (x₁ + x₂)/2, (y₁ + y₂)/2

(4 + 9)/2, (1 + 4)/2  =  (8 + t)/2, (2 + 3)/2

13/2, 5/2  =  (8 + t)/2, 5/2

Equating x coordinates, we get

8 + t  =  13

t  =  13 - 8

t  =  5

Problem 7 :

Find the ratio in which the line segment joining the points A (– 3, 10) and B (6, – 8) is divided by the point  P (– 1, 6).

Solution :

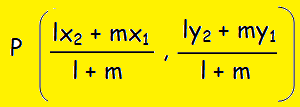
[l(6) + m(-3)]/(l + m), [l(-8) + m(10)]/(l + m)  =  (-1, 6)

(6l - 3m)/(l + m),  (-8l + 10m)/(l + m)  =  (-1, 6)

Equating the x coordinates, we get

6l - 3m  =  -1(l + m)

6l + l  =  -m + 3m

7l  =  2m

l/m  =  2/7

l : m  =  2 : 7

So, the required ratio is 2 : 7.

Problem 8 :

Find the coordinates of point A, where AB is the diameter of a circle with center is (2, – 3) and the coordinate of  B is (1, 4).

Solution :

Center is (2, -3). Let A(a, b) the required point.

Midpoint of diameter  =  Center

Midpoint  =  (x₁ + x₂)/2, (y₁ + y₂)/2

(1 + a)/2, (-3 + b)/2  =  (2, -3)

By equating x and y coordinate, we get

So, the required point is (1, -3).

Problem 9 :

Find the area of the triangle whose vertices are 

(1,–1), (–4, 6) and (–3, –5)

Solution :

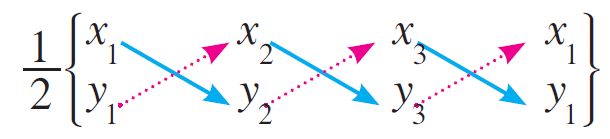
Area of triangle ABC

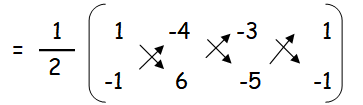
  =  (1/2)[(6 + 20 + 3) - (4 - 18 - 5)]

  =  (1/2)[29 - (-19)]

  =  (1/2)[29 + 19]

  =  (1/2) 48

  =  24 square units

Problem 10 :

Find the equation of the straight line through (1, 3) and parallel to the straight line 5x - 3y + 1 = 0.

Solution :

Equation of the line parallel to the given line :

Slope of the required line  =  Slope of the given line

m  =  -coefficient of x/coefficient of y

m  =  5/3

(y - y1)  =  m(x - x1)

(y - 3)  =  (5/3)(x - 1)

3y - 9  =  5x - 5

5x - 3y  - 5 + 9  =  0

5x - 3y + 4  =  0  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.