10th GRADE MATH PRACTICE PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
The sum of an infinite G.P is 4 and the sum of the cubes of the terms is 192. Determine the common ratio.
Solution :
Geometric series :
a, ar, ar2, ar3, ..................
Sum of infinite series = 4
a/(1-r) = 4
a3/(1-r)3 = 64
a3/(1-r)(1 - 2r + r2) = 64----(1)
Sum of cubes of terms of geometric series :
a3, (ar)3, (ar2)3, (ar3)3, ..................
a3, a3r3, a3r6, a3r9, ..................
Sum of cubes = 192
a3/(1-r3) = 192
a3/(1-r)(1+r+r2) = 192 ----(2)
(1) / (2)
a3/(1-r)(1-2r+r2) / a3/(1-r)(1+r+r2) = 64/192
(1+r+r2)/(1 - 2r + r2) = 1/3
(1-2r+r2) / (1+r+r2) = 3
1-2r+r2 = 3(1+r+r2)
2r2 + 5r + 2 = 0
2r2 + 4r + r + 2 = 0
2r(r + 2) + 1(r + 2) = 0
(2r + 1)(r + 2) = 0
r = -1/2 and r = -2
The required common ratios are -1/2 and -2.
Problem 2 :
A triangle with sides 3 cm, 4 cm and 5 cm is rotated about the side of length 4 cm. Find the volume of the solid generated.
Solution :
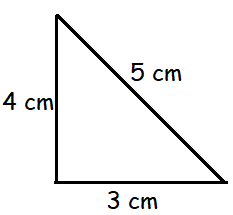
Height of the triangle = 4 cm and base = 3 cm
When we rotate the triangle, we will get cone.
Area of the triangle = (1/3) ⋅ πr2h
= (1/3) ⋅ π(3)24
= 12π
= 12 cm3
Problem 3 :
If A = {1, 3, 5, 7}, B = {1, 2, 4, 6, 8} and C = {1, 3, 6, 8} then find (A ∪ B) ∩ (A ∪ C).
Solution :
A ∪ B = {1, 3, 5, 7} U {1, 2, 4, 6, 8}
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8}
(A ∪ C) = {1, 3, 5, 7} U {1, 3, 6, 8}
(A ∪ C) = {1, 3, 5, 6, 7, 8}
(A ∪ B) ∩ (A ∪ C) = {1, 2, 3, 4, 5, 6, 7, 8}n{1, 3, 5, 6, 7, 8}
(A ∪ B) ∩ (A ∪ C) = {1, 3, 5, 6, 7, 8}
Problem 4 :
Let A = {0, 1} and B = {1, 3} be two sets. Let f: A→B be a function given by f(x) = 2x + 1. Represent this function as a set of ordered pairs.
Solution :
f(x) = 2x + 1
If x = 0, then f(0) = 1
If x = 1, then f(1) = 3
Required function = {(0, 1) (1, 3)}.
Problem 5 :
The sum of three numbers is 24. Among them one number is equal to half of the sum of the other two numbers but four times the difference of them. Find the numbers.
Solution :
Let x, y and z be three numbers.
x + y + z = 24 -----(1)
x = (y + z)/2
2x - y - z = 0 -----(2)
x = 4(y - z)
x - 4y + 4z = 0-----(3)
(1) + (2)
3x = 24
x = 8
By applying the value of x in x = (y + z)/2, we get
y + z = 16 ----(4)
By applying the value of x in 4(y - z), we get
y - z = 2 ----(5)
(4) + (5)
2y = 18
y = 9
By applying the value of y in (4), we get
9 + z = 16
z = 7
So, the values of x, y and z are 8, 9 and 7 respectively.
Problem 6 :
Find the remainder when 6x4 - 11x3 + 5 x2 - 7x + 9 is divided by (2x-3).
Solution :
Let p(x) = 6x4 - 11x3 + 5 x2 - 7x + 9
2x-3 = 0
x = 3/2
p(3/2) = 6(3/2)4-11(3/2)3+5(3/2)2-7(3/2)+9
= 6(81/16)-11(27/8)+5(9/4)-(21/2)+9
= 243/8 - 297/8 + 45/4 - 21/2 + 9
= (243 - 297 + 90 - 84 + 72)/8
= 24/8
= 3
So, the remainder is 3.
Problem 7 :
If 2, x, 26 are in arithmetic progression. Find the value of x.
Solution :
If the sequence is in arithmetic progression. then
a2 - a1 = a2 - a1
x-2 = 26-x
x + x = 26+2
2x = 28
x = 14
Problem 8 :
Determine the value of m if x+1 is a factor of
x3+mx2+19x+12
Solution :
p(x) = x3+mx2+19x+12
x + 1 = 0
x = -1
p(-1) = (-1)3+m(-1)2+19(-1)+12
-1+m-19+12 = 0
-20+m+12 = 0
-8+m = 0
m = 8
Problem 9 :
Find the square root of x2 + 10 x + 25
Solution :
√x2 + 10 x + 25 = √x2 + 2⋅x⋅5 + 25
= √(x + 5)2
= |x+5|
Problem 10 :
The age of the father is square of his daughter Henna. Five years hence the father is three times as old as Henna. Find the present ages of henna.
Solution :
Let x be the age of Henna.
Age of his father = x2
Age after 5 years,
Henna's age = x + 5
Father's age = x2 + 5
x2 + 5 = 3(x + 5)
x2 -3x+5-15 = 0
x2 -3x-10 = 0
(x-5)(x+2) = 0
x = 5 and x = -2
So, present age of Henna is 5.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

