ANGLE BISECTOR THEOREM EXAMPLE PROBLEMS
Angle bisector theorem :
The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the corresponding sides containing the angle.
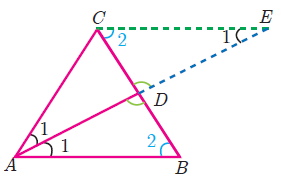
In ΔABC, AD is the internal bisector
AB/AC = BD/CD
Example 1 :
In a
triangle ABC,AD is the internal bisector of angle A, meeting BC at D.
(i) If BD = 2 cm, AB = 5 cm, DC = 3 cm find AC.
Solution :
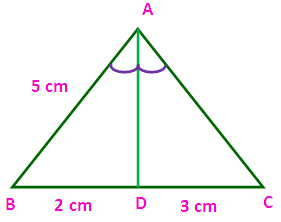
Using “Angle bisector theorem” in the triangle ABC, we get
(AB/AC) = ( BD/DC)
(5/AC) = (2/3)
AC = (3 ⋅ 5)/2
= 15/2
= 7.5 cm
(ii) If AB = 5.6 cm, AC = 6 cm and DC = 3 cm find BC.
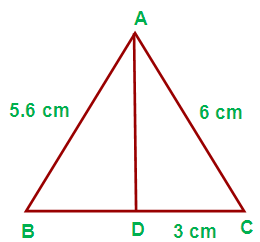
Solution :
Using “Angle bisector theorem” in the triangle ABC, we get
(AB/AC) = (BD/DC)
(5.6/6) = (BD/3)
BD = (5.6 ⋅ 3)/6
= 16.8/6
= 2.8 cm
From this we need to find the value of BC
BC = BD + DC
= 2.8 + 3
. = 5.8 cm
(iii) If AB = x, AC = x – 2 cm, BD = x + 2 cm and DC = x – 1 find the value of x
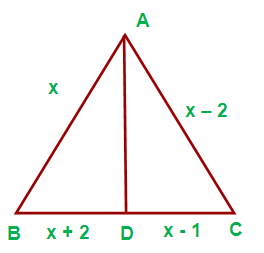
Solution :
Using “Angle bisector theorem” in the triangle ABC, we get
(AB/AC) = (BD/DC)
[x/(x – 2)] = [(x + 2)/(x - 1)]
x (x – 1) = (x + 2) (x – 2)
x ² – x = x ² – 4
x² – x - x² + 4 = 0
- x + 4 = 0
- x = - 4
x = 4 cm
The value of x is 4 cm
Verifying Angle Bisector Theorem in Given Triangle
Example 2 :
Check whether AD is the bisector of angle A of the triangle ABC in each of the following.
(i) AB = 4 cm, AC = 6 cm, BD = 1.6 cm and CD = 2.4 cm
Solution :
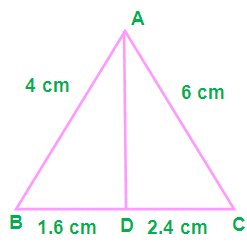
To check whether AD is the bisector of angle A of the triangle ABC, we have to check the following condition
(AB/AC) = (BD/DC)
(4/6) = (1.6/2.4)
0.66 = 0.66
From this we come to know that AD is the bisector of angle A of the triangle ABC.
(ii) AB = 6 cm, AC = 8 cm, BD = 1.5 cm and CD = 3 cm
Solution :
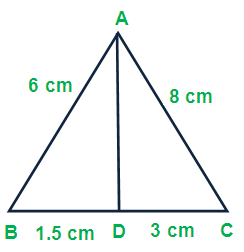
To check whether AD is the bisector of angle A of the triangle ABC, we have to check the following condition
(AB/AC) = (BD/DC)
(6/8) = (1.5/3)
0.75 ≠ 0.5
Hence, AD is not the bisector of angle A of the triangle ABC.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Writing Quadratic Functions in Standard Form
Apr 26, 24 12:39 PM
Writing Quadratic Functions in Standard Form or Vertex Form -
Factoring Quadratic Trinomials
Apr 26, 24 01:51 AM
Factoring Quadratic Trinomials - Key Concepts - Solved Problems -
Factoring Trinomials Worksheet
Apr 25, 24 08:40 PM
Factoring Trinomials Worksheet
