VERIFYING BASIC PROPORTIONALITY THEOREM EXAMPLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
In the figure given below, if LM ∥ CB and LN ∥ CD prove that AM/AB = AN/AD.
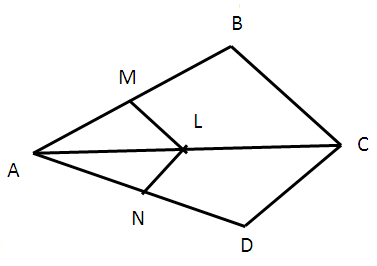
Solution :
In triangle ABC
LM is parallel to BC
AM/MB = AL/LC ------- (1)
NL is parallel to DC
AN/ND = AL/LC ------(2)
(1) = (2)
AM/MB = AN/ND
Hence proved.
Example 2 :
In the figure given below, DE ∥ AC and DF ∥ AE. prove that BF/FE = BE/EC.
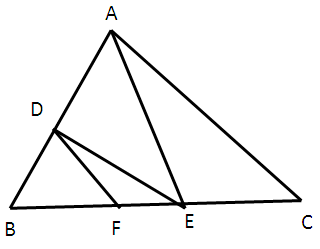
Solution :
In triangle ABC,
The side DE and AC are parallel. So, we have
BD/DA = BE/EC -----(1)
In triangle AEB,
The side DF and AE are parallel. So, we have
BD/DA = BF/FE -----(2)
(1) = (2)
BE/EC = BF/FE
Hence proved.
Example 3 :
In the figure given below, DE ∥ OQ and DF ∥ OR. Show that EF ∥ QR.
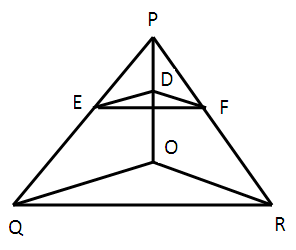
Solution :
In triangle PQO,
The sides DE and OQ are parallel. So, we have
PE/EQ = PD/DO----(1)
In triangle POR,
The sides DE and OQ are parallel. So, we have
PF/FR = PD/DO ------(2)
(1) = (2)
PE/EQ = PF/FR
By converse of BPT theorem, EF is parallel to QR.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 1)
Feb 05, 26 09:37 AM
Digital SAT Math Problems and Solutions (Part - 1) -
AP Precalculus Problems and Solutions
Feb 05, 26 06:41 AM
AP Precalculus Problems and Solutions -
SAT Math Preparation with Hard Questions
Feb 05, 26 05:30 AM
SAT Math Preparation with Hard Questions

