AREA OF TRIANGLE USING THREE COORDINATES WORKSHEET

Problem 1 :

Find the area of the triangle whose vertices are 

(1,–1), (–4, 6) and (–3, –5)

Solution

Problem 2 :

Find the area of the triangle whose vertices are 

(-10, -4) (-8, -1) and (-3, -5)

Solution

Problem 3 :

Determine whether the sets of points are collinear.

(-1/2, 3), (-5, 6) and (-8, 8)

Solution

Problem 4 :

Determine whether the sets of points are collinear.

(a, b + c), (b, c + a) and (c, a + b)

Solution

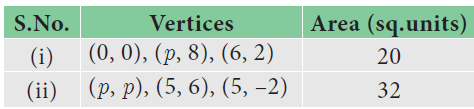
Problem 5 :

Find the value of p in each case. 

Solution

Problem 6 :

If the area of the triangle formed by the vertices A(-1 , 2), B (k ,-2) and C(7, 4) (taken in order) is 22 sq. units, find the value of k.

Solution

Problem 7 :

If the points P(-1, -4), Q(b, c) and R(5, -1) are collinear and if 2b + c = 4, then find the values of b and c.

Solution

Problem 8 :

The floor of a hall is covered with identical tiles which are in the shapes of triangles. One such triangle has the vertices at (-3, 2), (-1, -1) and (1, 2). If the floor of the hall is completely covered by 110 tiles, find the area of the floor.

Solution

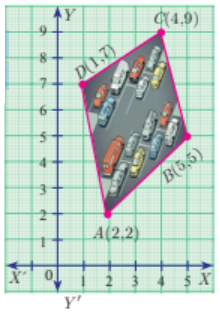
Problem 9 :

The given diagram shows a plan for constructing a new parking lot at a campus. It is estimated that such construction would cost $1300 per square feet. What will be the total cost for making the parking lot?

Solution

Vertices of the triangle taken in order and their areas are given below. In each of the following find the value of a.

Problem 1 :

Whose vertices are (0, 0), (4, a) and (6, 4) and its area is 17 sq.units

Solution

Problem 2 :

The vertices are (a, a) , (4 , 5) and ( 6 , -1) and its area is 9 sq. units

Solution

Problem 3 :

The vertices are (a, -3),(3, a) and (-1, 5) and its area is 12 sq.units

Solution

Vertices of given triangles are taken in order and their areas are provided aside. In each case, find the value of ‘p’.

Problem 4 :

The vertices are (0, 0), (p, 8), (6, 2) and has the area of 20 square units.

Solution

Problem 5 :

The vertices are (p, p), (5, 6), (5, –2) and has the area of 32 square units.

Solution

Problem 6 :

The area of triangle formed by the points (−5,0) , (0,−5) and (5,0) is 

(A) 0 sq.units     (B) 25 sq.units     (C) 5 sq.units

(D) none of these

Solution

Problem 7 :

If (5, 7), (3, p) and (6, 6) are collinear, then the value of p is

(A) 3     (B) 6     (C) 9     (D) 12

Solution

In each of the following, find the value of ‘a’ for which the given points are collinear.

Problem 8 :

(2, 3), (4, a) and (6, –3)

Solution

Problem 9 :

(a, 2 – 2a), (–a + 1, 2a) and (–4 – a, 6 – 2a)

Solution

Problem 1 :

If the three points (h, 0) (a, b) and (0, k) lie on a straight line, then using the area of the triangle formula show that (a/h) + (b/k) = 1, where h, k ≠ 0

Solution

Problem 2 :

Find the area of the triangle formed by joining the midpoints of the sides of a triangle whose vertices are (0, -1) (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.

Solution

Problem 3 :

If the points A(-3, 9), B (a, b) and C(4, -5) are collinear and if a + b = 1, then find a and b.

Solution

Problem 4 :

The area of a triangle is 5 sq.units. Two of its vertices are (2, 1) and (3, –2). The third vertex is (x, y) where

y = x + 3

Find the coordinates of the third vertex.

Solution

Problem 5 :

Find the area of a triangle formed by the lines 3x + y - 2 = 0, 5x + 2y - 3 = 0 and 2x - y - 3 = 0

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.