HOW TO FIND VERTICAL ASYMPTOTE OF A FUNCTION
Vertical Asymptote :
This is a vertical line that is not part of a graph of a function but guides it for y-values 'far' up and/or 'far' down.
The graph may cross it but eventually, for large enough or small enough values of y, that is
y ----> ±∞
Always, the graph would get closer and closer to the horizontal asymptote without touching it.
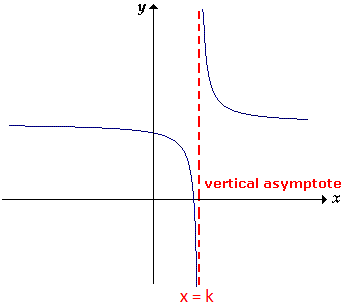
In the diagram above, x = k is an horizontal asymptote. Because, the graph is getting closer and closer to x = k without touching it as y ----> ±∞.
We will be able to find vertical asymptotes of a function, only if it is a rational function.
That is, the function has to be in the form of
f(x) = g(x)/h(x)
Rational Function - Example :
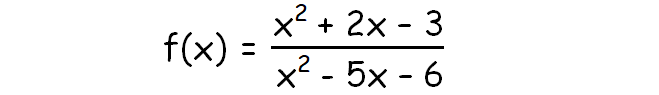
Steps to Find the Equation of a Vertical Asymptote of a Rational Function
Step 1 :
Let f(x) be the given rational function. Make the denominator equal to zero.
Step 2 :
When we make the denominator equal to zero, suppose we get x = a and x = b.
Step 3 :
The equations of the vertical asymptotes are
x = a and x = b
In each case, find the equation of vertical asymptote :
Example 1 :
f(x) = 1/(x + 6)
Solution :
Step 1 :
In the given rational function, the denominator is
x + 6
Step 2 :
Equate the denominator to zero and solve for x.
x + 6 = 0
x = - 6
Step 3 :
The equation of the vertical asymptote is
x = - 6
Example 2 :
f(x) = (x2 + 2x - 3)/(x2 - 5x + 6)
Solution :
Step 1 :
In the given rational function, the denominator is
x2 - 5x + 6
Step 2 :
Equate the denominator to zero and solve for x.
x2 - 5x + 6 = 0
(x - 2)(x - 3) = 0
x - 2 = 0 or x - 3 = 0
x = 2 or x = 3
Step 3 :
The equations of two vertical asymptotes are
x = 2 and x = 3
Example 3 :
f(x) = (2x - 3)/(x2 - 4)
Solution :
Step 1 :
In the given rational function, the denominator is
x2 - 4
Step 2 :
Equate the denominator to zero and solve for x.
x2 - 4 = 0
x2 - 22 = 0
(x + 2)(x - 2) = 0
x = -2 or x = 2
Step 3 :
The equations of two vertical asymptotes are
x = -2 and x = 2
Example 4 :
f(x) = (2x - 3)/(x2 + 4)
Solution :
Step 1 :
In the given rational function, the denominator is
x2 + 4
Step 2 :
Equate the denominator to zero and solve for x.
x2 + 4 = 0
x2 = -4
x = ±√-4
x = ±2i
x = 2i or x = -2i (Imaginary)
Step 3 :
When we equate the denominator to zero, we don't get real values for x.
So, there is no vertical asymptote.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Trigonometry Sum and Difference Identities
May 07, 24 09:17 AM
Trigonometry Sum and Difference Identities - Concept - Solved Problems -
Trigonometry Even and Odd Iidentities
May 05, 24 12:25 AM
Trigonometry Even and Odd Iidentities -
SOHCAHTOA Worksheet
May 03, 24 08:50 PM
SOHCAHTOA Worksheet