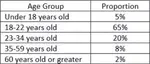
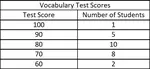
TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Two acute angles are complementary to each other if their sum is equal to 90°. In a right triangle the sum of the two acute angles is equal to 90°. So, the two acute angles of a right triangle are always complementary to each other.
Let ABC be a right triangle, right angled at B.
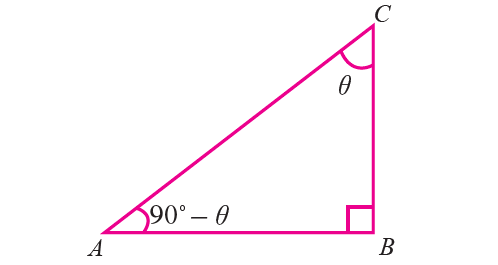
If ∠ACB = θ, then ∠BAC = 90° - θ and hence the angles ∠BAC and ∠ACB are complementary
For the angle θ, we have
|
sin θ = AB/AC cos θ = BC/AC tan θ = AB/BC |
cosec θ = AC/AB sec θ = AC/BC cot θ = BC/AB |
Similarly, for the angle (90° - θ), we have
|
cos (90 - θ) = AB/AC sin (90 - θ) = BC/AC tan (90 - θ) = BC/AB |
cosec (90 - θ) = AC/AB sec (90 - θ) = AC/BC cot (90 - θ) = AB/BC |
Comparing the equations in (1) and (2) we get,
sin θ = AB/AC = cos (90 - θ)
cos θ = BC/AC = sin (90 - θ)
tan θ = AB/BC = cot (90 - θ)
cosec θ = AC/AB = sec (90 - θ)
sec θ = AC/BC = cosec (90 - θ)
cot θ = BC/AB = tan (90 - θ)
Trigonometric Ratios of Complementary Angles
|
sin θ = cos (90 - θ) cos θ = sin (90 - θ) tan θ = cot (90 - θ) |
cosec θ = sec (90 - θ) sec θ = cosec (90 - θ) cot θ = tan (90 - θ) |
Question 1 :
Evaluate
cos 56° / sin 34°
Answer :
The angles 56° and 34° are complementary.
Use trigonometric ratios of complementary angles.
cos 56° / sin 34° = cos 56° / cos (90° - 34°)
cos 56° / sin 34° = cos 56° / cos 56°
cos 56° / sin 34° = 1
Question 2 :
Evaluate
tan 25° / cot 65°
Answer :
The angles 25° and 65° are complementary.
Use trigonometric ratios of complementary angles.
tan 25° / cot 65° = tan 25) / tan (90° - 65°)
tan 25° / cot 65° = tan 25° / tan 25°
tan 25° / cot 65° = 1
Question 3 :
Evaluate
(cos 65° sin 18° cos 58°)/(cos 72° sin 25° sin 32°)
Answer :
Use trigonometric ratios of complementary angles.
cos 65° = cos (90° - 25°) = sin 25°
sin 18° = sin (90° - 72°) = cos 72°
cos 58° = cos (90° - 32°) = sin 32°
(cos 65° sin 18° cos 58°) / (cos 72° sin 25° sin 32°) is
= (sin 25° cos 72° sin 32°) / (cos 72° sin 25° sin 32°)
= 1
So,
cos 65° sin 18° cos 58°)/(cos 72° sin 25° sin 32° = 1
Question 4 :
Evaluate :
tan 35° tan 60° tan 55° tan 30°
Answer :
tan 35° = tan (90° - 55°) = cot 55° = 1/tan 55°
tan 60° = tan (90° - 30°) = cot 30° = 1/tan 30°
tan 35° tan 60° tan 55° tan 30° :
= (1/tan 55° ) x (1/tan 30°) tan 55° tan 30°
= 1
So,
tan 35° tan 60° tan 55° tan 30° = 1
Question 5 :
If sin A = cos 33°, find A.
Answer :
sin A = cos 33°
sin A = sin (90° - 33°)
sin A = sin 57°
A = 57°
Question 6 :
If tan A tan 35° = 1, find A.
Answer :
tan A tan 35° = 1
Divide each side by tan 35°.
tan A = 1/tan 35°
tan A = cot 35°
tan A = tan (90° - 35°)
tan A = tan 55°
A = 55°
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 47)
Mar 05, 26 09:19 PM
Digital SAT Math Problems and Solutions (Part - 47) -
Digital SAT Math Problems and Solutions (Part - 46)
Mar 05, 26 08:37 PM
Digital SAT Math Problems and Solutions (Part - 46) -
Digital SAT Math Problems and Solutions (Part - 45)
Mar 05, 26 08:02 PM
Digital SAT Math Problems and Solutions (Part - 45)