TYPES OF SOLUTIONS OF PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
In this section, we will learn the types of solution of a pair of linear equations are having. By comparing the coefficients of linear equations, we may find what type of solution they have.
To compare the coefficients of linear equations in two variables, the equations must be in the form.
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
The following three cases are possible for any given system of linear equations.
(i) a1/a2 ≠ b1/b2, we get a unique solution
(ii) a1/a2 = a1/a2 = c1/c2, there are infinitely many solutions.
(iii) a1/a2 = a1/a2 ≠ c1/c2, there is no solution
Example 1 :
Which of the following pairs of linear equations has unique solution, no solution, infinitely many solutions. In case there is unique solution, find it by using cross multiplication method.
(i) x – 3y – 3 = 0
3x – 9y – 2 = 0
Solution :
From the above information, let us take the values of a1, a2, b1, b2, c1 and c2
a1 = 1, b1 = -3, c1 = -3
a1 = 3, b1 = -9, c1 = -2
a1/a2 = 1/3
b1/b2 = -3/(-9) = 1/3
c1/c2 = -3/(-2) = 3/2
Here a1/a2 = b1/b2 ≠ c1/c2
From this we can decide the given lines are parallel.
(ii) 2x + y = 5
3x + 2y = 8
Solution :
2x + y – 5 = 0
3x + 2y – 8 = 0
From the above information, let us take the values of a1, a2, b1, b2, c1 and c2
a1 = 2, b1 = 1, c1 = -5
a1 = 3, b1 = 2, c1 = -8
a1/a2 = 2/3
b1/b2 = 1/2
c1/c2 = (-5)/(-8) = 5/8
Here, a₁/a₂ ≠ b₁/b₂
Therefore two given lines are intersecting
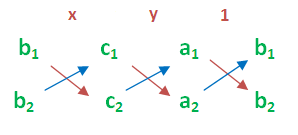
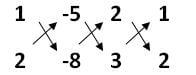
x/(-8 + 10) = y/(-15 + 16) = 1/(4 – 3)
x/2 = y/1 = 1/1
x/2 = 1 y/1 = 1
x = 2 y = 1
(iii) 3x – 5y = 20
6x – 10y = 40
Solution :
3 x – 5 y – 20 = 0 --------(1)
6 x – 10 y – 40 = 0 --------(2)
From the above information, let us take the values of a1, a2, b1, b2, c1 and c2
a1 = 3, b1 = -5, c1 = -20
a1 = 6, b1 = -10, c1 = -40
a1/a2 = 3/6 = 1/2
b1/b2 = -5/(-10) = 1/2
c1/c2 = (-20)/(-40) = 1/2
here, a1/a2 = b1/b2 = c1/c2
Therefore the two given lines are coincident.
(iv) x – 3y – 7 = 0
3x – 3y – 15 = 0
Solution :
From the above information, let us take the values of a1, a2, b1, b2, c1 and c2
a1 = 1, b1 = -3, c1 = -7
a1 = 3, b1 = -3, c1 = -15
a₁/a ₂ = 1/3
b₁/b ₂ = -3/(-3) = 1
c₁/c ₂ = (-7)/(-15) = 7/15
here, a1/a2 ≠ b1/ b2
So, the given two lines are intersecting.
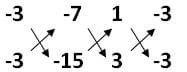
x/(45 - 21) = y/(-21 + 15) = 1/(-3+9)
x/24 = y/(-6) = 1/6
x/24 = 1/6 y/(-6) = 1/6
x = 24/6 y = -6/6
x = 4 y = -1
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Trigonometry Sum and Difference Identities
May 07, 24 09:17 AM
Trigonometry Sum and Difference Identities - Concept - Solved Problems -
Trigonometry Even and Odd Iidentities
May 05, 24 12:25 AM
Trigonometry Even and Odd Iidentities -
SOHCAHTOA Worksheet
May 03, 24 08:50 PM
SOHCAHTOA Worksheet