CURVED SURFACE AREA OF CONE

Curved surface area of cone is the measurement of outer area,where the extension of bottom portion wont be included. 

Curved surface area of cone

Cone is a solid or hollow object which tapers from a circular or roughly circular base to a point.

CSA of cone = πrl

"r" and "l" stands for radius and slant height of cone.

Example 1 :

If the vertical angle and the radius of the right circular cone are 60 degree and 15 cm respectively, then find its slant height and curved surface area.

Solution :

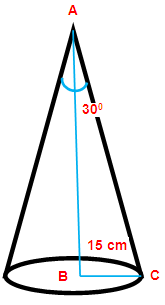
Vertical angle of the  right circular cone = 60°

radius of the cone (r) = 15 cm

In the triangle ABC, ∠ABC = 30°

 BC = 15 cm

Opposite side (BC) = 15 cm

Adjacent side (AB) = ?

Hypotenuse side (AC) = ?

here,  we need to find the measurement of the side AC. So we have to use sinθ.

sin θ = Opposite side/Hypotenuse side

sin 30° = BC/AC      

(1/2) = 15/AC

AC = 30 cm

Slant height (L) = 30 cm

Curved surface area of cylinder  =  π r l

=  π ⋅ 15 ⋅ 30 

=  450 π cm²

So, curved surface area of cone is 450 π cm²

Example 2 :

If the circumference of the base of the solid right circular cone is 236 and its slant height is 12 cm, find its curved surface area.

Solution :

Circumference of the base  =  236 cm

Slant height (L)  =  12 cm

2 Π r  =  236

Πr  =  236/2

Π r  =  118

Curved surface area of cone  =  Π r l

=  118 (12) 

=  1416 cm²

So, curved surface area of cone is 1416 cm²

Question 3 :

A heap of paddy is in the form of a cone whose diameter is 4.2 m and height is 2.8 m. If the heap is to be covered exactly by a canvas to protect it from rain, then find the area of the canvas needed.

Solution :

Diameter of heap of paddy  =  4.2 m

r  =  4.2/2

r  =  2.1 m

height of paddy (h) = 2.8 m

 l²  =  r²+h²

l  =  √(2.1)²+(2.8)² 

l  =  √(4.41+7.84)

l  =  √12.25

l  =  √(3.5 ⋅3.5)

l  =  3.5 cm

Curved surface area of heap of paddy  =  Π r l

=  (22/7) ⋅ 2.1 ⋅ 3.5

=  22 ⋅ 2.1 ⋅ 0.5

=  23.1 cm²

So, curved surface area of paddy is 23.1 cm².

Example 4 :

The central angle and radius of a sector of a circular disc are 180 degree and 21 cm respectively. If the edges of the sector are joined together to make a hollow cone, then find the radius of the cone.

Solution :

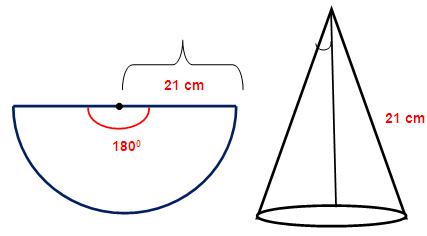
The cone is being created by joining the radius. So the radius of the sector is going to be the slant height of the cone.

Slant height L  =  21 cm

Arc length of the sector  =  Circumference of the base of the cone

 Length of arc = (θ/360) ⋅ 2Π R

Here R represents radius of the sector

=  (180/360)  ⋅ 2 ⋅ (22/7) ⋅ 21

=  (1/2) ⋅ 2 ⋅ 22 ⋅ 3

=  66 cm

So, circumference of the base of the cone = 66

2 Π r  =  66

2 ⋅ (22/7) ⋅ r = 66

r  =  10.5 cm

So, radius of the cone is 10.5 cm.

Example 5 :

Radius and slant height of a solid right circular cone are in the ratio 3:5. If the curved surface area is 60Π cm², then find its radius and slant height.

Solution :

Radius and slant height of a solid right circular cone are in the ratio 3:5.

r : L  =  3 : 5 

r / L  =  3/5

r  =  3L/5

Curved surface area of cone  =  60 Πcm² 

Π r L  =  60Π

Π ⋅ (3L/5) ⋅ L  =  60Π

l²  =  60 Π ⋅ (1/Π) ⋅ (5/3)

l²  =  60 ⋅ (5/3)

l²  =  100

l  =  10 cm

r  =  3(10)/5

r  =  30/5

r  =  6 cm

So, radius and slant height of cone are 6 cm and 10 cm respectively.

Example 6 :

A sector containing an angle of 120 degree is cut off from a circle of radius 21 cm and folded into a cone. Find the curved surface area of a cone.

Solution :

The cone is being created by joining the radius. So the radius of the sector is going to be the slant height of the cone.

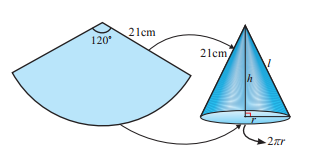
Slant height (l)  =  21 cm

Arc length of the sector  =  Circumference of the base of the cone

Length of arc  =  (θ/360) ⋅ 2Π R

Here R represents radius of the sector

=  (120/360) ⋅ 2 ⋅ (22/7) ⋅ 21

=  (1/3) ⋅ 2 ⋅ 22 ⋅ 3

=  44 cm

So, circumference of the base of the cone = 44

2Πr  =  44

2 ⋅ (22/7) ⋅ r  =  44

r   =  7 cm

Now, we need to find the curved surface area of cone 

Curved surface area of cone  =  Πrl

=  (22/7) x 7 x 21 

=  462 cm²

So, curved surface area is 462 cm². 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.