MODE IN STATISTICS

Mode is one of the measures of central tendency which can be defined as follows.

For a given set of observations, mode may be defined as the value that occurs the maximum number of times.

Thus, mode is that value which has the maximum concentration of the observations around it. This can also be described as the most common value with which, even, a layman may be familiar with.

Thus, if the observations are 5, 3, 8, 9, 5 and 6, then Mode (Mo) = 5 as it occurs twice and all the other observations occur just once.

The definition for mode also leaves scope for more than one mode. Thus sometimes we may come across a distribution having more than one mode. Such a distribution is known as a multi-modal distribution. Bi-modal distribution is one having two modes.

Furthermore, it also appears from the definition that mode is not always defined. As an example,

If the marks of 5 students are 50, 60, 35, 40, 56, there is no modal mark as all the observations occur once i.e. the same number of times. 

We may consider the following formula for computing mode from a grouped frequency distribution:

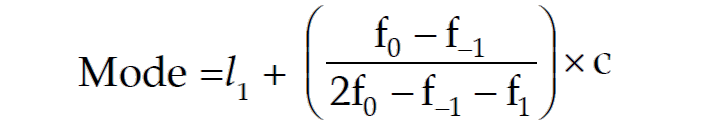
where,

l₁ = LCB of the modal class

f₀ = frequency of the modal class

f_-1 = frequency of the pre modal class

f₁ = frequency of the post modal class

C = class length of the modal class

Practice Problem

Compute the mode for the following distribution

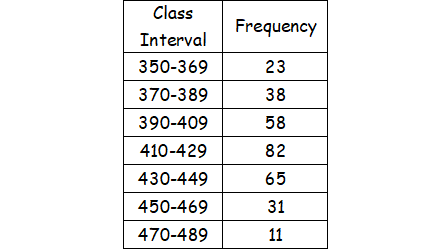
Solution :

Computation of mode :

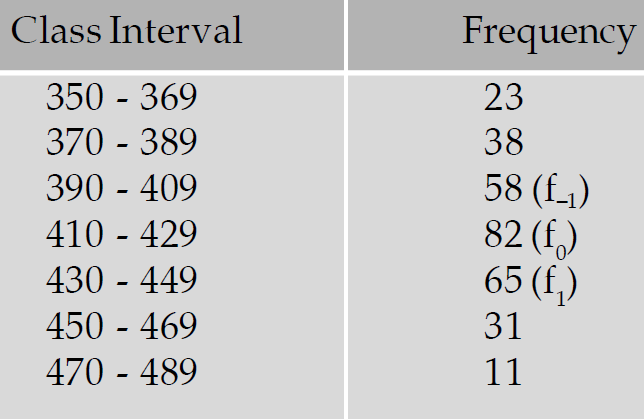
For the given data, the formula to find mode is given by 

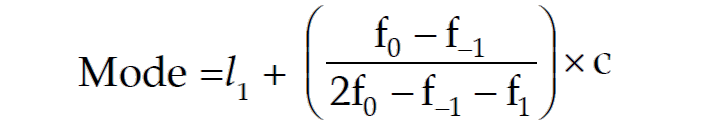
Going through the frequency column, we note that the highest frequency i.e. f₀ is 82.

Then, f_-1 = 58 and f₁ = 65.

Also, the modal class i.e. the class against the highest frequency is (410 - 419). 

Thus, 

l₁ = LCB = 409.50

C = 429.50 - 409.50 = 20

C = 429.50 – 409.50 = 20

Substitute these values in the above formula.

Mode = 409.50 + [(82 - 58)/(2 ⋅ 52 - 58 - 65)] ⋅ 20

= 409.50 + 11.71

= 421.21

Relation between Mean Median and Mode

When it is difficult to compute mode from a grouped frequency distribution, we may consider the following empirical relationship between mean, median and mode :

Mean - Mode = 3(Mean - Median)

or

Mode = 3median - 2mean

The above result holds for holds for a moderately skewed distribution.

Note :

If y = a + bx, then we have

mode of y = a + b(mode of x) 

For example, if y = 2 + 1.50x and mode of x is 15, then 

mode of y = 2 + 1.50(mode of x)

= 2 + 1.50 ⋅ 15

=  2 + 22.50

= 24.50

Properties of Mode

1. Although mode is the most popular measure of central tendency, there are cases when mode remains undefined.

2. Unlike mean, it has no mathematical property.

3. Mode is affected by sampling fluctuations.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.