ANGLE OF ELEVATION TRIGONOMETRY PROBLEMS

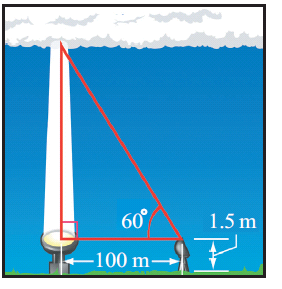
Problem 1 :

To find the cloud ceiling, one night an observer directed a spotlight vertically at the clouds. Using a theodolite placed 100 m from the spotlight and 1.5 m above the ground, he found the angle of elevation to be 60°. How high was the cloud ceiling? (Hint : See
figure)

cloud is present. The cloud ceiling at airports  must be sufficiently high for safe take offs and landings. At night the cloud ceiling can be determined by illuminating the base of the clouds by a spotlight pointing vertically upward.)

Solution :

The side which is opposite to 90 degree is known as hypotenuse side, the side which is opposite to θ is known as opposite side and the remaining side is known as adjacent side.

In the given problem,we have to find the length of opposite side. 

AC = Hypotenuse side

AB = Opposite side

BC = Adjacent side

tan θ = opposite side/adjacent side

tan 60°  =  AB/BC

√3  =  AB/100

100 √3  =  AB

AB  =  100 √3

=  100 (1.732)  =  173.2

Height of ceiling from ground  =  173.2 + 1.5  =  174.7 m 

Problem 2 :

A simple pendulum of length 40 cm subtends 60° at the vertex in one full oscillation. What will be the shortest distance between the initial position and the final position of the bob? (between the extreme ends)

Solution :

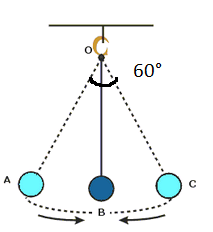
In triangle OBC  angle BOC = 30°

BC - opposite side

OC - hypotenuse side = 40 cm

AB - adjacent side

length of pendulum = 40 cm

sin θ = opposite side/hypotenuse side

sin 30° = BC/OC

1/2 = BC/40

40 = 2 BC

BC  =  20 cm

length of AC = 2(BC) = 2(20) = 40 cm

Problem 3 :

Two crows A and B are sitting at a height of 15 m and 10 m in two different trees vertically opposite to each other. They view a bread (an eatable) on the ground at an angle of depression 45° and 60° respectively. They start at the same time and fly at the same speed along the shortest path to pick up the bread. Which bird will succeed in it?

Solution :

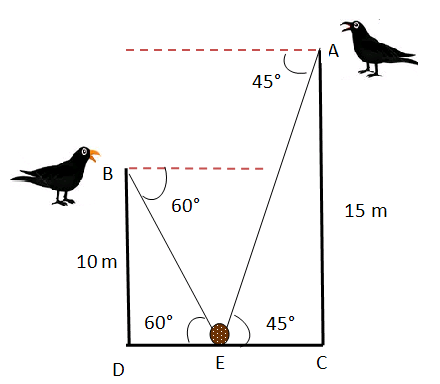
In the given problem,we have to the length of AE and BE.

In triangle BED

 BE - hypotenuse side

BD - opposite side

sin θ  =  Opposite side/Hypotenuse side

sin 60°  =  BD/BE

√3/2  =  10/BE

BE√3  =  10 x 2

BE  =  20/√3  = 11.55 m

In triangle AEC,

 AC - opposite side = 15 m

  AE - hypotenuse side

sin θ = Opposite side/Hypotenuse side

sin 45° = AC/AE

1/√2 = 15/AE

AE = 15√2

= 21.21 m

The distance of BD is shorter than AE. So, bird "B" is having chance to succeed.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.