SYNTHETIC DIVISION

Synthetic division is the method that can be used to divide polynomials. The advantage of this method is that it allows one to calculate without writing variables, than long division.

To use this method in polynomial division, the divisor must be of first degree.

Example 1 : 

Find the quotient and remainder when

p(x)  =  3x³ - 2x² - 5 + 7x

is divided by d(x)  =  x + 3. 

Solution :

Step 1 :

Arrange dividend and the divisor in standard form.

Then, 

3x³ - 2x² + 7x - 5     (standard form of dividend)

x + 3     (standard form of divisor)

Write the coefficients of dividend in the first row.

Put ‘0’ for missing term(s).

3     -2     7     -5     (first row)

Step 2 :

Find out the zero of the divisor.

x + 3  =  0 

x  =  -3

Step 3 : 

Write the zero of divisor in front of dividend in the first row.

Put ‘0’ in the first column of second row.

Step 4 : 

Complete the second row and third row as shown below.

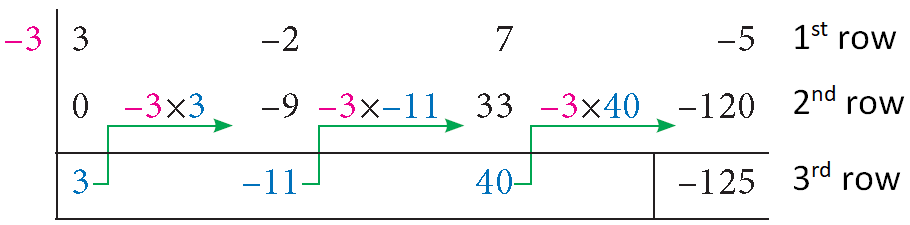
All the entries except the last one in the third row are the coefficients of the quotient.

Therefore, the quotient is

3x² - 11x + 40

and the remainder is

-125

Example 2 :

Find the quotient and remainder : 

(x³ + x² - 3 x + 5) ÷ (x - 1) 

Solution :

Arrange dividend and the divisor in standard form.

Then, 

x³ + x² - 3x + 5     (standard form of dividend)

x - 1     (standard form of divisor)

Find out the zero of the divisor.

x - 1  =  0 

x  =  1

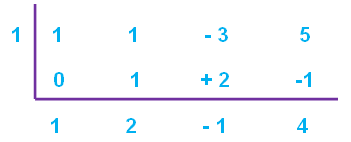
Therefore, the quotient is

x² + 2x - 1

and the remainder is

4

Example 3 :

Find the quotient and remainder : 

(3x³ - 2x² + 7x - 5) ÷ (x + 3) 

Solution :

Arrange dividend and the divisor in standard form.

Then, 

3x³ - 2x² + 7x - 5     (standard form of dividend)

x + 3     (standard form of divisor)

Find out the zero of the divisor.

x + 3  =  0 

x  =  -3

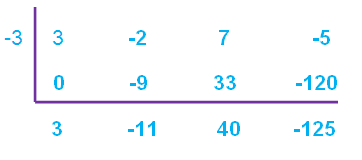
Therefore, the quotient is

3x² - 11x + 40

and the remainder is

-125

Example 4 :

Find the quotient and remainder : 

(3x³ + 4x² - 10x + 6) ÷ (3x - 2)

Solution :

Arrange dividend and the divisor in standard form.

Then, 

3x³ + 4x² - 10x + 6     (standard form of dividend)

3x - 2     (standard form of divisor)

Find out the zero of the divisor.

3x - 2  =  0 

x  =  2/3

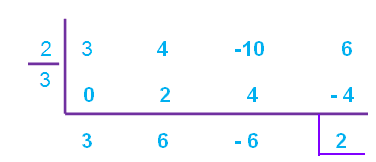
Therefore, the quotient is

3x² + 6x - 6

and the remainder is

2

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here

If you have any feedback about our math content, please mail us : 

v4formath@gmail.com

We always appreciate your feedback. 

You can also visit the following web pages on different stuff in math. 

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractrions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6