INTEGRATION USING PARTIAL FRACTIONS EXAMPLES

Integration Using Partial Fractions Examples :

Here we are going to see some example problems in integration using the concept of partial fractions.

Integration Using Partial Fractions Examples

Example 1 :

Integrate the following function with respect to x :

1/(x - 1) (x + 2)²

Solution :

Decompose the given rational function into partial fractions. 

1/(x - 1) (x + 2)²  =  A/(x - 1) + B/(x + 2) + C/(x + 2)²

1  =  A(x+2)² + B(x-1)(x+2) + C(x-1)

Plug x = 1

1  =  9A

A  =  1/9

Plug x = -2

1  =  C(-3)

C  =  -1/3

Plug x = 0

1  =  4A-2B-C

1  =  4(1/9) - 2B - (-1/3)

1  =  (4/9)- 2B + (1/3)

1 - (4/9) - (1/3)  =  -2B

-2B  =  (9 - 4 - 3)/9

-2B  =  2/9

B  =  -1/9

Integrate.

∫[1/(x - 1) (x + 2)²] dx

=  (1/9)∫(1/(x-1))dx-(1/9)∫(1/(x+2)-(1/3)∫(1/(x+2)² dx

=  (1/9)log(x-1) - (1/9)log (x+2)-(1/3)(1/(x+2)) + c

=  (1/9) [log(x - 1) - log(x + 2)] - (1/3)(1/(x+2)) + c

=  (1/9) [log(x - 1)/(x - 2)] - (1/3(x + 2)) + c

Example 2 :

Integrate the following function with respect to x :

(3x - 9)/(x - 1)(x + 2)(x² + 1)

Solution :

Decompose the given rational function into partial fractions. 

(3x - 9)/(x - 1)(x + 2)(x² + 1) 

  =  A/(x - 1) + B/(x + 2) + (Cx + D)/(x² + 1)

3x - 9  =  A(x+2)(x²+1)+B(x-1)(x²+1)+(Cx+D)(x-1)(x+2)

Plug x = 1

3 - 9  =  A(6)

-6  =  6A  ==>  A  =  -1

Plug x = -2

-6 - 9  =  B(-3)(5)

-15  =  -15B  ==>  B  =  1

Plug x = 0

- 9  =  2A - B - 2D

-9  =  2(-1) - 1 - 2D

-9  + 3  =  -2D

-6  =  -2D

D  =  3

3x - 9  =  A(x+2)(x²+1)+B(x-1)(x²+1)+(Cx+D)(x-1)(x+2)

Plug x = -1

- 12  =  A(1)(2) + B(-2)(2) + (-C+D)(-2)

-12  =  2A - 4B + 2C - 2D

-12  =  2(-1) - 4(1) + 2C - 2(3)

-12  =  -2 - 4 - 6 + 2C

2C  =  -12 + 12

C  =  0

Integrate.

∫[(3x - 9)/(x - 1)(x + 2)(x² + 1)] dx

  =   -∫1/(x - 1) dx + ∫1/(x + 2) dx + ∫ 3/(x² + 1) dx

  =  - log (x - 1) + log (x + 2) + 3 tan^-1(x)

  =  log (x + 2)/(x - 1) + 3  tan^-1(x) + c

Example 3 :

Integrate the following function with respect to x :

x³/(x - 1)(x - 2)

Solution :

x³/(x - 1)(x - 2)  =  x³/(x² - 3x + 2)

In the given rational fraction, the highest exponent of x in numerator is greater than the highest exponent of x in denominator. 

So, we can use long division to decompose the given rational function. 

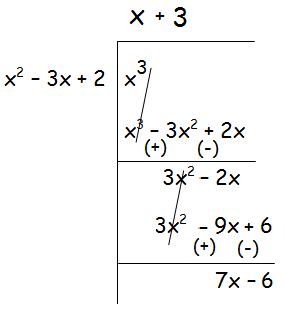
From the above long division, we have

x³/(x - 1)(x - 2)  =  (x + 3) + (7x - 6)/(x² - 3x + 2)

x³/(x - 1)(x - 2)  =  (x + 3) + (7x - 6)/(x - 1)(x - 2) ----(1)

Decompose (7x - 6)/(x - 1)(x - 2) into partial fractions. 

(7x - 6)/(x - 1)(x - 2)  =  A/(x - 1) + B(x - 2)

Simplify.

7x - 6  =  A(x - 2) + B(x - 1)

Plug x = 1

7(1) - 6  =  A(1 -2 ) + B(1 - 1)

1  =  A(-1)

A  =  -1

Plug x = 2

7(2) - 6  =  A(2 -2 ) + B(2 - 1)

8  =  B(1)

B  =  8

Therefore we have

(1)-----> x³/(x - 1)(x - 2)  =  (x + 3) - 1/(x - 1) + 8/(x - 2)

Integrate. 

∫[x³/(x - 1)(x - 2)] dx

  =  ∫(x + 3) dx -∫1/(x - 1) dx + 8∫1/(x - 2) dx

=  x²/2 + 3x -  log(x - 1) + 8log(x -  2) + C

After having gone through the stuff given above, we hope that the students would have understood, how to integrate rational functions using partial fractions. 

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.