FRACTIONS IN MATHEMATICS

In simple words, a fraction is the part of a whole. 

In fractions (for example 17/23), the number above the line (17) is called numerator and the number below the line (23) is called denominator. 

The numerator represents a number of equal parts, and the denominator, which cannot be zero, indicates how many of those parts make up a unit or a whole.

For example, in the fraction 3/4, the numerator, 3, tells us that the fraction represents 3 equal parts, and the denominator, 4, tells us that 4 parts make up a whole. 

The picture given below illustrates the fraction 3/4. 

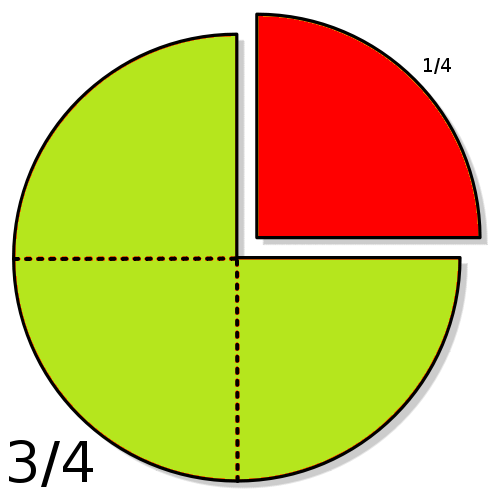
Different Types of Fractions

Within the world of fractions, we do have several types and ways of writing them. Let's discuss these now.

Proper fraction :

A fraction is called a proper fraction if its

Denominator > Numerator.

Example : 3/4, 1/2, 9/10, 5/6

Improper fraction :

A fraction is called an improper fraction if its

Numerator > Denominator.

Example : 5/4, 6/5, 41/30, 51/25

Mixed fraction :

A fraction consisting of a natural number and a proper fraction is called a mixed fractions.

Example : 2 3/4, 1 4/5, 5 1/7

Like Fractions:

In two or more fractions, the denominators (bottom numbers) are same, they are called as like fractions.

Examples : 3/5 , 6/5, 2/5, 7/5

In the above fractions, all the denominators are same. That is 5.

Unlike Fractions :

In two or more fractions, the denominators (bottom numbers) are different, they are called as unlike fractions.

Examples : 3/5 , 6/7, 2/9, 7/2

In the above fractions, all the denominators are different. They are 5, 7, 9 and 2.

Converting Improper Fraction to Mixed Fraction

The picture shown below illustrates how to convert an improper fraction to mixed fraction. 

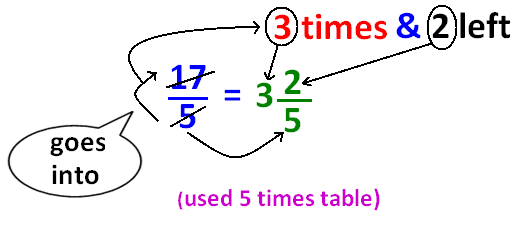
Converting Mixed Fraction to Improper Fraction

The picture shown below illustrates how to convert a mixed fraction to improper fraction.

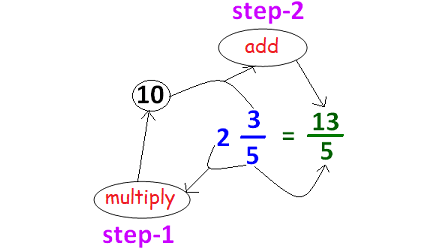
Addition and Subtraction of Fractions with Same Denominator

Example 1 : 

Simplify : 2/5 + 3/5

Solution : 

Here, for both the fractions, we have the same denominator, we have to take only one denominator and add the numerators. 

Then, we get 

2/5 + 3/5  =  (2 + 3) / 5

2/5 + 3/5  =  5/5

2/5 + 3/5  =  1

Example 2 :

Simplify : 7/5 - 3/5

Solution : 

Here, for both the fractions, we have the same denominator, we have to take only one denominator and subtract the numerators. 

Then, we get 

7/5 - 3/5  =  (7-3) / 5

7/5 - 3/5  =  4/5

Addition and Subtraction of Fractions with Different Denominators

Here, we explain two methods to add two fractions with different denominators.

1)  Cross-multiplication method

2)  L.C.M method

Cross-Multiplication Method :

If the denominators of the fractions are co-prime or relatively prime, we have to apply this method.

Fro example, let us consider the two fractions 1/8,  1/3.

In the above two fractions, denominators are 8 and 3.

For 8 and 3, there is no common divisor other than 1. So 8 and 3 are co-prime.

Here we have to apply cross-multiplication method to add the two fractions 1/8 and 1/3 as given below. 

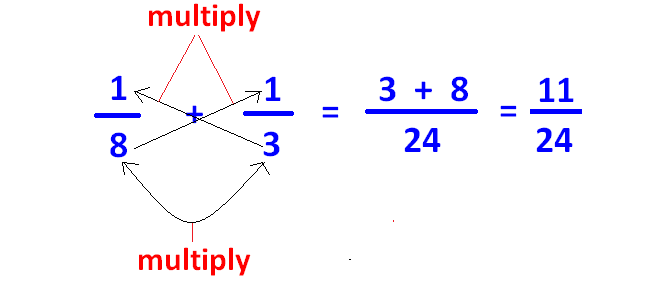
L.C.M Method :

If the denominators of the fractions are not co-prime (there is a common divisor other than 1), we have to apply this method.

Fro example, let us consider the two fractions 5/12,  1/20.

In the above two fractions, denominators are 12 and 20.

For 12 and 20, if there is at least one common divisor other than 1, then 12 and 20 are not co-prime.

For 12 & 20, we have the following common divisors other than 1.

2 and 4

So 12 and 20 are not co-prime.

In the next step, we have to find the L.C.M (Least common multiple) of 12 and 20.

12  =  2² ⋅ 3

20  =  2² ⋅ 5

When we decompose 12 and 20 in to prime numbers, we find 2, 3 and 5 as prime factors for 12 and 20. 

To get L.C.M of 12 and 20, we have to take 2, 3 and 5 with maximum powers found above.

So, L.C.M of 12 and 20 is

=  2² ⋅ 3 ⋅ 5

=  4 ⋅ 3 ⋅ 5

=  60

Now we have to make the denominators of both the fractions to be 60 and add the two fractions 5/12 and 1/20 as given below.

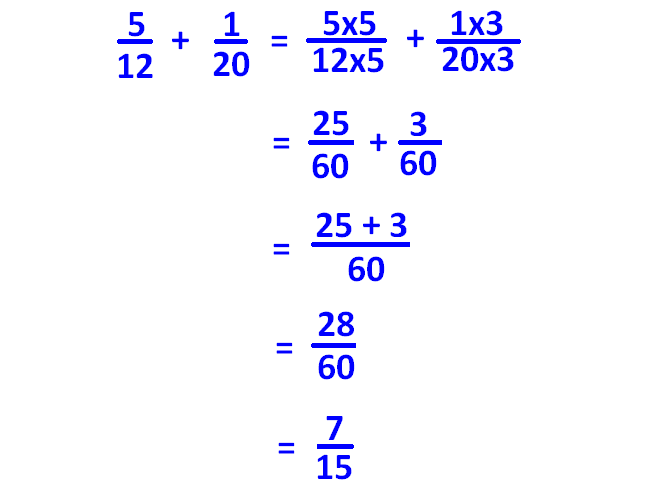
Note :

We have to do the same process for subtraction of two fractions with different denominators. 

Multiply a Fraction by a Whole Number

To multiply a proper or improper fraction and a whole number,first, we have to multiply the whole number and numerator of the fraction, keeping the denominator same.

For example, 

2 ⋅ 3/5   =  6/5

3 ⋅  7/11  =  21/11

To multiply a mixed fraction by a whole number, first convert the mixed fraction to an improper fraction and proceed as explained above.

For example, 

4 ⋅ 3 4/7   =  4 ⋅ 25/7

4 ⋅ 3 4/7  =  (4 ⋅ 25)/7

4 ⋅ 3 4/7  =  100/7

4 ⋅ 3 4/7  =  14 2/7

Multiply a Fraction by a Fraction

To multiply a proper or improper fraction by another proper or improper fraction, we have to multiply the numerators and denominators. 

For example, 

2/3 ⋅ 4/5   =  8/15

1/3 ⋅  7/11  =  7/33

Divide a Whole Number by a Fraction 

To divide a whole number by any fraction, multiply the whole number by the reciprocal of the fraction.

For example, 

6 ÷ 2/5  =  6 ⋅ 5/2

6 ÷ 2/5  =  (6 ⋅ 5)/2

6 ÷ 2/5  =  (3 ⋅ 5)/1

6 ÷ 2/5  =  15  

Divide a Fraction by a Whole Number

To divide a fraction by a whole number, we have to multiply the denominator of the fraction by the whole number and simplify, if possible. 

For example, 

2/5 ÷ 6  =  2/(5 ⋅ 6)

2/5 ÷ 6  =  1/(5 ⋅ 3)

2/5 ÷ 6  =  1/15

Divide a Whole Number by a Mixed Fraction 

While dividing a whole number by a mixed fraction, first convert the mixed fraction into improper fraction and proceed.

For example, 

6 ÷ 3 4/5  =  6 ÷ 19/5

6 ÷ 3 4/5  =  6 ⋅ 5/19

6 ÷ 3 4/5  =  (6 ⋅ 5)/19

6 ÷ 3 4/5  =  30/19

Divide a Fraction by a Fraction

To divide a fraction by another fraction, multiply the first fraction by the reciprocal of the second fraction.

For example,

1/5 ÷ 3/7  =  1/5 ⋅ 7/3

1/5 ÷ 3/7  =  (1 ⋅ 7) / (5 ⋅ 3)

1/5 ÷ 3/7  =  7/15

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.