EQUATION OF LINE WORKSHEET

1. Find the general equation of a line whose slope is 3 and y-intercept is 4.

2. Find the general equation of a line passing through the point (3, 0) with slope -6.

3. Find the general equation of a line passing through the point (2, 5) with slope -5.

4. Find the general equation of a line passing through the points (-1, 1) and (2, -4). 

5. If the x-intercept and y-intercept of a line are 2/3 and 3/4 respectively, find the general equation of the line. 

6. Find the equation of a line which is parallel to x-axis and passing through the point (2, 3).

7. Find the general equation of a line which is parallel to the line 3x - 7y = 12 and passing through the point (6, 4).

8. Find the equation of a line which is perpendicular to the line y = (4/3)x - 7 and passing through the point (7, –1).

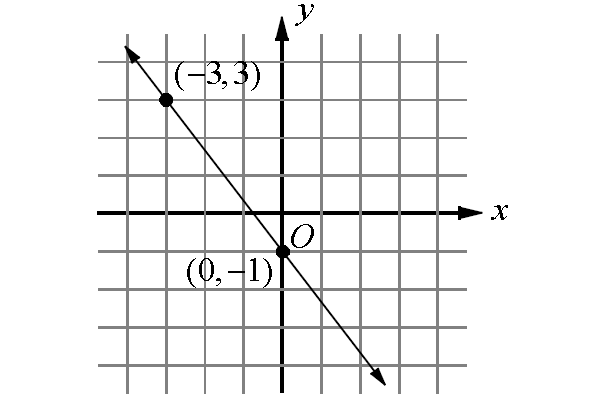
9. Find the equation of line in slope-intercept form. 

10. Cost of producing 10 dolls is $160 and that of 25 dolls is $385. Assuming the cost curve to be linear, find the cost of 50 dolls. 

Answers

1. Answer :

Given : slope is 3 and y-intercept is 4.

Equation of a line in slope-intercept form :

y = mx + b

Substitute m = 3 and b = 4.

y = 3x + 4

Subtract y from each side.

0 = 3x - y + 4

3x - y + 4 = 0

2. Answer :

Given : point (3, 0) and slope = -6.

Equation of line in point-slope form :

y - y₁ = m(x - x₁)

Substitute (x₁ , y₁) = (3 , 0) and m = -6.

y - 0 = -6(x - 3)

Simplify.

y = -6x + 18

Add 6x to each side. 

6x + y = 18

Subtract 18 from each side.

6x + y - 18 = 0

3. Answer :

Given : point (2, 5) and slope = -5.

y = mx + b

Substitute m = -5.

y  =  -5x + b ----(1)

Substitute (x, y) = (2, 5).

5 = -5(2) + b

Simplify.

5 = -10 + b

Add 10 to each side.

15 = b

Substitute 15 in (1).

(1)----> y = -5x + 15

Add 5x to each side.

5x + y = 15

Subtract 15 from each side.

5x + y - 15 = 0

4. Answer :

Given : Two points on the straight line : (-1, 1) and  (2, -4).

Equation of line in two-points form :

(y - y₁)/(y₂ - y₁) = (x - x₁)/(x₂ - x₁)

Substitute (x₁ , y₁) = (-1, 1) and (x₂, y₂) = (2, -4).

(y - 1)/(-4 - 1) = (x + 1)/(2 + 1)

Simplify.

(y - 1)/(-5) = (x + 1)/3

Cross multiply.

3(y - 1) = -5(x + 1)

3y - 3 = -5x - 5

5x + 3y + 2 = 0

5. Answer :

Given : x-intercept is 2/3 and y-intercept is 3/4.

Equation of straight line in intercept form :

x/a  +  y/b = 1

Substitute a = 2/3 and b = 3/4.

x/(2/3) + y/(3/4) = 1

Simplify.

3x/2 + 4y/3 = 1

(9x + 8y)/6 = 1

Multiply each side by 6.

9x + 8y = 6

Subtract 6 from each side.

9x + 8y - 6 = 0

6. Answer :

Given : Required line is parallel to x-axis and passing through the poi point (2, 3).

Equation of line parallel to x-axis :

y = k -----(1)

The line is passing through (2, 3).

So, substitute (x, y) = (2, 3).

3 = k

Substitute k = 3 in (1).

y = 3

7. Answer :

Given : Required line is parallel to 3x - 7y = 12 and passing through the poi point (6, 4).

Equation of line parallel to 3x - 7y = 12 :

3x - 7y + k = 0 -----(1)

The line is passing through (6, 4).

So, substitute (x, y) = (6, 4).

3(6) - 7(4) + k = 0

Simplify.

18 - 28 + k = 0

-10 + k = 0

Add 10 to each side.

k = 10

Substitute k = 10 in (1).

(1)----> 3x - 7y + 10 = 0

8. Answer :

Given : Required line is perpendicular to y = (4/3)x - 7 and passing through the poi point (7, -1).

Write the equation y  =  (4/3)x - 7 in general form.

y = (4/3)x - 7

Multiply each side by 3.

3y = 4x - 21

Subtract 3y from each side. 

0 = 4x - 3y - 21

4x - 3y - 21  =  0

Equation of a line perpendicular to 4x - 3y - 21 = 0.

3x + 4y + k = 0 ----(1)

The line is passing through (7, -1).

So, substitute (x, y) = (7, -1).  

3(7) + 4(-1) + k = 0

Simplify.

21 - 4 + k = 0

17 + k = 0

Subtract 17 from each side. 

k = -17

Substitute k = -17 in (1).

(1)----> 3x + 4y - 17 = 0

9. Answer :

The given line is a falling line. So, its slope will be a negative value.

Measure the rise and run. 

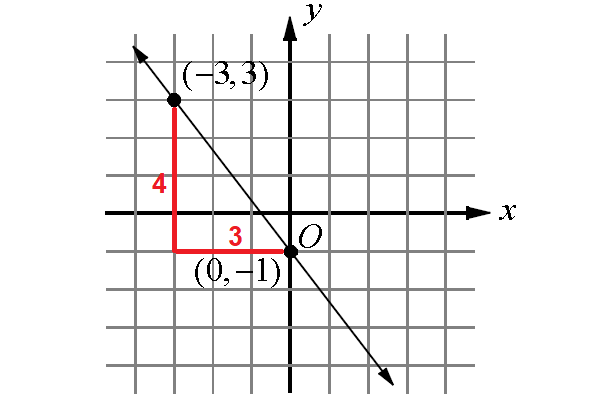
From the above diagram, rise = 4 and run = 3.

slope = rise/run

= -4/3

The line in the diagram above intersects y-axis at -1.

So, y-intercept is -1. 

Equation of the line in slope intercept form :

y = mx + b

Substitute m = -4/3 and b = -1. 

y = -4x/3 - 1

10. Answer :

Given : Cost of 10 dolls is $160, 25 dolls is $385 and the cost curve is linear.  

Since the cost curve is linear, the function which best fits the given information is equation of line in slope-intercept form.

y = Ax + B

y ----> Total cost

x ----> Number of dolls

Target : Find the cost 25 dolls. That is, the value of y when x = 95.

From the given information, 

x = 10, y = 160

x = 25, y = 385

Substitute the above values of x and y in y = Ax + B.

160 = 10A + B

385 = 25A + B

Solv for A and B.

A = 15, B = 10

Cost curve :

y = 15x + 10

Substitute x = 50.

y = 15(50) + 10

= 750 + 10

= 760

So, the cost of 50 dolls is $760.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.