NATURE OF THE ROOTS OF A QUADRATIC EQUATION

In this section, we will examine the roots of a quadratic equation.

That is, we will analyze whether the roots of a quadratic equation are equal or unequal,  real or imaginary and rational or irrational. 

To examine the roots of a quadratic equation, let us consider the general form a quadratic equation.

 ax² + bx + c = 0

(Here a, b and c are real and rational numbers)

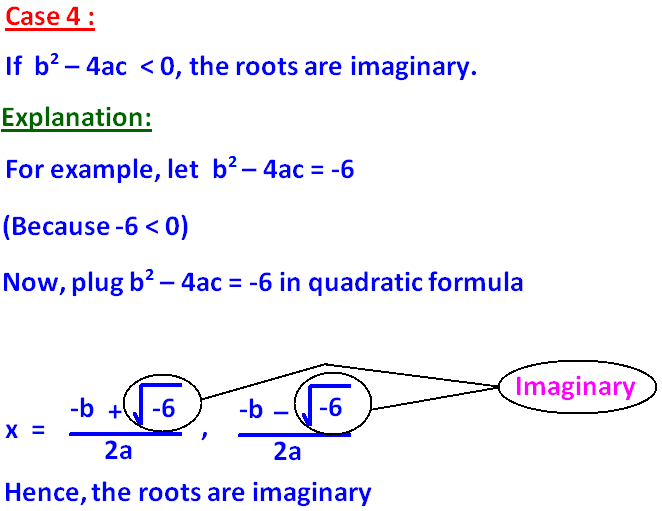
To know the nature of the roots of a quadratic-equation, we will be using the discriminant b² - 4ac.

Because b² - 4ac discriminates the nature of the roots.

Let us see how this discriminant b² - 4ac can be used to know the nature of the roots of a quadratic-equation.

Examples 1-4 : Examine the nature of the roots of each of the following quadratic equations.

Example 1 :

8x² - 7x - 1 = 0

Solution :

The given quadratic equation is in general form.

Comparing ax² + bx + c = 0 and 8x² - 7x - 1 = 0,

a = 8, b = -7, c = -1

Find the value of the discriminant b² - 4ac.

b² - 4ac = (-7)² - 4(8)(-1)

= 49 + 32 

= 81

or

= 9²

b² - 4ac = 81 > 0 and also a perfect square. 

So, the roots are real, unequal and rational.

Example 2 :

x² - 3x - 1 = 0 

Solution :

The given quadratic equation is in general form

Comparing ax² + bx + c = 0 and x² - 3x - 1 = 0,

a = 1, b = -3, c = -1

Find the value of the discriminant b² - 4ac. 

b² - 4ac = (-3)² - 4(1)(-1)

= 9 + 4

= 13 

Here, b² - 4ac = 13 > 0, but not a perfect square. 

So, the roots are real, unequal and irrational.

Example 3 :

x² - 26x + 169 = 0

Solution :

The given quadratic equation is in general form.

Comparing ax² + bx + c = 0 and x² - 3x - 1 = 0,

a = 1, b = -26, c = 169

Find the value of the discriminant b² - 4ac. 

b² - 4ac = (-26)² - 4(1)(169)

= 676 - 676

= 0

Since b² - 4ac = 0, the roots are real, equal and rational.

Example 4 : 

¹⁄₍ₓ ₋ ₇₎ + ³⁄₍ₓ ₊ ₄₎ = 1

Solution :

The given quadratic equation is not in general form. 

Writing the given quadratic equation in general form :

¹⁄₍ₓ ₋ ₇₎ + ³⁄₍ₓ ₊ ₄₎ = 1

Multiply both sides of the equation by (x - 7)(x + 4) to get rid of the denominators on the left side.

(x - 7)(x + 4)(¹⁄₍ₓ ₋ ₇₎ + ³⁄₍ₓ ₊ ₄₎) = 1(x - 7)(x + 4)

Using Distributive Property,

(x + 4) + 3(x - 7) = (x - 7)(x + 4)

x + 4 + 3x - 21 = x² - 3x - 28

4x - 17 = x² - 3x - 28

0 = x² - 7x - 11

or

x² - 7x - 11 = 0

Now, the quadratic equation is in general form

Comparing ax² + bx + c = 0 and x² - 7x - 11 = 0,

a = 1, b = -7, c = -11

Find the value of the discriminant b² - 4ac.

b² - 4ac = (-7)² - 4(1)(-11)

= 49 + 44

= 93

Here, b² - 4ac > 0, but not a perfect square. 

So, the roots are real, unequal and irrational.

Example 5 :

9x² - 6x  + k = 0

If the roots of the above quadratic equation are real, equal and rational, find the value of k.

Solution :

The given quadratic equation is in general form

Comparing ax² + bx + c = 0 and 9x² - 6x  + k = 0,

a = 9, b = -6, c = k

Since the roots are real, equal and rational, the value of the discriminant 'b² - 4ac' must be zero. 

b² - 4ac = 0

Substitute a = 9, b = 6 and c = k.

6² - 4(9)k = 0

36 - 36k = 0

Subtract 36 from both sides.

-36k = -36

Divide both sides by -36.

k = 1

Example 6 : 

6x = 2 - y

y = x² + 11

Find the number ordered pairs (x, y) in the xy-plane are solutions to the system of equations above?

A) 0

B) 1

C) 2

D) Infinitely Many

Solution :

6x = 2 - y ----(1)

y = x² + 11 ----(2)

In (1), solve for y in terms of x. 

6x = 2 - y

Add y to both sides.

6x + y = 2

Subtract 6x from both sides.

y = 2 - 6x

Multiply both sides by 2.

y = 2 - 6x

Substitute y = 2 - 6x in (2).

2 - 6x = x² + 11

x² + 6x + 9 = 0

Comparing ax² + bx + c = 0 and x² + 6x + 9 = 0,

a = 1, b = 6 and c = 9

Find the value of the discriminant b² - 4ac.

b² - 4ac = 9² - 4(1)(8)

b² - 4ac = 81 - 32

b² - 4ac = 49

Since b² - 4ac = 49 > 0, the roots are real and unequal. It means, there are real values for x. Hence, there will be two real values for y.

Therefore, two ordered pairs in the xy-plane are solutions to the given system of equations.

The correct answer choice is (C).

Example 7 :

3x² - 6x + m = 0

If the quadratic equation above has two real roots, find all possible values of m.

Solution :

Comparing ax² + bx + c = 0 and 3x² - 6x + m = 0,

a = 3, b = -6 and c = m

Since the given quadratic has two real roots, the value of the discriminant 'b² - 4ac' must be greater than zero. 

b² - 4ac > 0

(-6)² - 4(3)(m) > 0

36 - 12m > 0

Subtract 36 from both sides. 

-12m > -36

Divide both sides by -12.

m < 3

Any real value less than 3 can be the value of m.

Click here to get detailed answers for the above questions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.