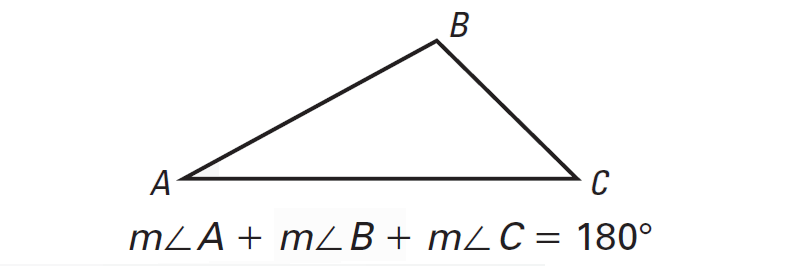CROSS MULTIPLICATION METHOD

This is one of the methods we use to solve system of linear equations.

Let us consider the following system of linear equations.

a₁x + b₁y + c₁ = 0

a₂x + b₂y + c₂ = 0

We have to write the coefficients of the equations and do cross multiplication as shown below.

We write the coefficient of y and constant term and two more columns by repeating the coefficients of x and y as follows.

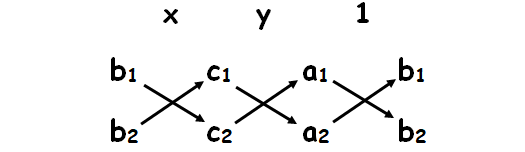
The result is given by

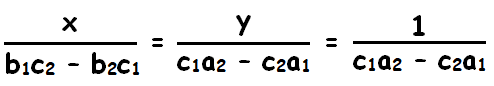
The solution is

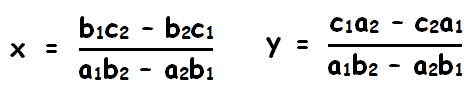
Example 1 :

Solve the following system of equations using cross multiplication method :

2x + 7y - 5 = 0

-3x + 8y = -11

Solution :

First we have to change the given linear equations in the form a₁x + b₁y + c₁  =  0, a₂x + b₂y + c₂  =  0.

2x + 7y - 5  =  0

-3x + 8y + 11  =  0

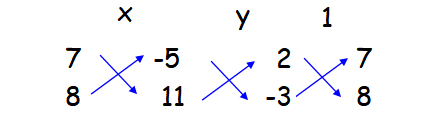
x/(77 + 40) = y/(15 - 22) = 1/[16 + 21]

x/117 = y/(-7) = 1/37

Therefore the solution is (117/37, -7/37).

Example 2 :

Solve the following system of equations using cross multiplication method :

3x + 4y = 24

20x - 11y = 47

Solution :

Write the given equations in the form of

a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0

3x + 4y - 24 = 0 ----(1)

20x - 11y - 47 = 0 ----(2)

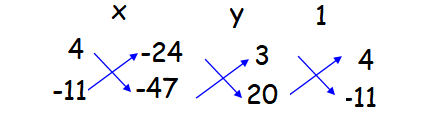
x/(-188 - 264) = y/(-480 - (-141)) = 1/(-33 - 80)

x/(-452) = y/(-480+141)) = 1/(-33-80)

x/(-452) = y/(-339) = 1/(-113)

Therefore solution is (4, 3).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.