ADDITION OF POLYNOMIALS

Consider the two polynomials given below

(5x² + 4x + 1) and  (2x² + 5x + 2)

We may use any one of the methods to add two polynomials.

(i)  Vertically

(ii)  Horizontally

In vertical form, align the like terms and add as shown below. 

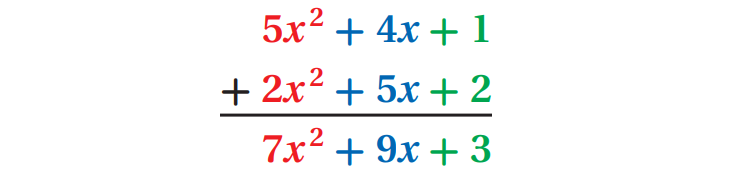
In horizontal form, use the Associative and Commutative properties to regroup like terms together and combine them as shown below.  

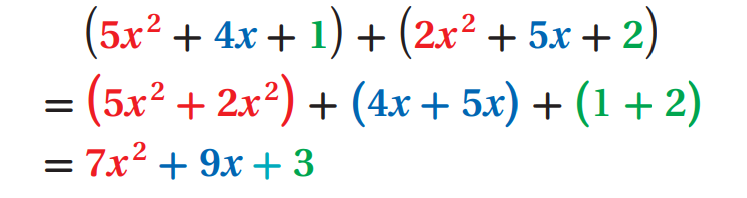
Question 1 :

Add

(5x⁴-3x²+4) + (6x³-4x²-7)

Solution :

=  (5x⁴-3x²+4) + (6x³-4x²-7)

Combining the like terms :

=  5x⁴+6x³-3x²-4x²+4-7

=  5x⁴+6x³+(-3x²-4x²)+(4-7)

=  5x⁴+6x³-7x²-3

Question 2 :

Add

(5x³-7x²+3x-4) + (8x³+2x²+3x-7)

Solution :

=  (5x³-7x²+3x-4) + (8x³+2x²+3x-7)

Combining the like terms :

= (5x³+8x³) + (-7x²+2x²)+(3x+3x)+(-4-7)

=  13x³-5x²+6x-11

Question 3 :

Find the perimeter of triangle given below.

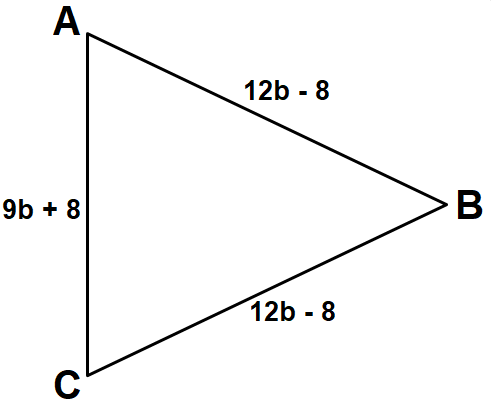
Solution :

Perimeter of triangle ABC  =  Sum of length of sides AB, BC, CA

Perimeter of triangle ABC  =  AB + BC + CA

AB  =  12b-8, BC  =  12b-8 and CA  =  9b+8

Perimeter of triangle ABC  =  12b-8+12b-8 +9b+8

=  12b+12b+9b-8-8+8

=  33b - 8

Question 4 :

Find the perimeter of triangle given below.

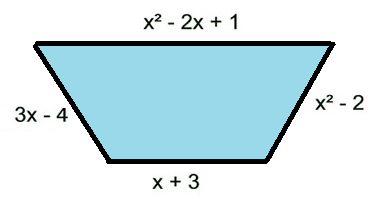
Solution :

By finding sum of length of all side, we get perimeter of the trapezium.

=  x²-2x+1+x²-2+x+3+3x-4

=  (x²+x²)+(-2x+x+3x)+(1-2+3-4)

=  2x²+2x-2

Question 5 :

The area of a parallelogram is 10x²+16x-8 square units. A circle has a radius of x units. A right triangle has legs of x units and x-1 units. Express the total area of all three shapes in terms of x and π).

Solution :

Area of parallelogram  =  10x²+16x-8  ------(1)

Area of circle  =  πr²

Here radius  =  x units

Area of circle  =  πx²  ------(2)

Area of triangle  =  (1/2) ⋅ base ⋅ height

=  (1/2) ⋅ x(x-1)

=  x²/2 - x/2  ------(3)

(1) + (2) + (3)

=  10x² + 16x - 8 + πx² + x²/2 - x/2

=  (10x²+πx²+x²/2) + 16x-x/2 - 8

=  x²(10+π+1/2) + x(16-1/2) - 8

=  x²[(20+2π+1)/2] + x[(32-1)/2] - 8

=  x²[(21+2π)/2] + x(31/2) - 8

So, the total area of the given shapes is 

x²[(21+2π)/2] + x(31/2) - 8

Question 6 :

The cost (in dollars) of making b bracelets is represented by 4 + 5b. The cost (in dollars) of making b necklaces is represented by 8b + 6.

Write a polynomial that represents how much more it costs to make b necklaces than b bracelets.

Solution :

The cost of making b bracelets = 4 + 5b

The cost b necklaces = 8b + 6

To find how much more is necklaces than bracelets, we have to subtract these two.

= (8b + 6) - (4 + 5b)

= 8b + 6 - 4 - 5b

= 8b - 5b + 6 - 4

= 3b + 2

Question 7 :

The number of individual memberships at a fitness center in m months is represented by 142 + 12m. The number of family memberships at the fitness center in m months is represented by 52 + 6m.

Write a polynomial that represents the total number of memberships at the fitness center.

Solution :

Number of individual membership = 142 + 12m

Number of family membership = 52 + 6m

Total number of memberships = 142 + 12m + 52 + 6m

Combining like terms, we get

= (142 + 52) + (12m + 6m)

= 194 + 18m

Question 8 :

You drop a ball from a height of 98 feet. At the same time, your friend throws a ball upward. The polynomials represent the heights (in feet) of the balls after t seconds.

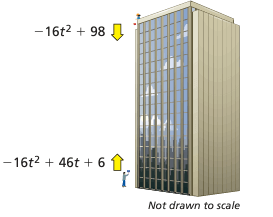
a. Before the balls reach the same height, write a polynomial that represents the distance between your ball and your friend’s ball after t seconds.

b. Interpret the coefficients of the polynomial in part (a).

Solution :

a) The distance between the balls :

= (-16t² + 98) - (-16t² + 46t + 6)

= -16t² + 98 + 16t² - 46t - 6

By combining the like terms, we get

= -16t² + 16t² - 46t - 6 + 98

= - 46t + 92

b) Coefficient of t = -46

constant = 92

Question 9 :

During a 7-year period, the amounts (in millions of dollars) spent each year on buying new vehicles N and used vehicles U by United States residents are modeled by the equations

N = −0.028t3 + 0.06t² + 0.1t + 17

U = −0.38t² + 1.5t + 42

where t = 1 represents the first year in the 7-year period.

a. Write a polynomial that represents the total amount spent each year on buying new and used vehicles in the 7-year period.

b. How much is spent on buying new and used vehicles in the fifth year?

Solution :

a) 

N = −0.028t³ + 0.06t² + 0.1t + 17

U = −0.38t² + 1.5t + 42

Total amount = −0.028t³ + 0.06t² + 0.1t + 17 + (−0.38t² + 1.5t + 42)

= −0.028t³ −0.38t² + 0.06t²+ 0.1t + 1.5t + 17 + 42

= −0.028t³ −0.32t² + 1.6t + 59

b)  

When t = 5,

= −0.028(5)³ −0.32(5)² + 1.6(5) + 59

= -3.5 - 8 + 8 + 59

= 55.5

So, they spent $55.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.