EXAMPLES ON INTERNAL AND EXTERNAL ANGLE BISECTOR THEOREM

Example 1 :

In a triangle MNO, MP is the external bisector of angle M meeting NO produced at P. IF MN = 10 cm, MO = 6 cm, NO - 12 cm, then find OP.

Solution :

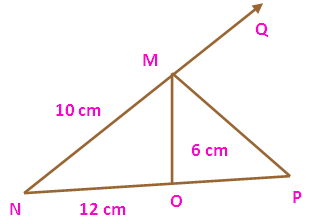
MP is the external bisector of angle M by using angle bisector theorem in the triangle MNO we get,

(NP/OP)  =  (MN/MO)

NP  =  NO + OP

  =  12 + OP

(12 + OP)/OP  =  10/6

6 (12 + OP)  =  10 OP

72 + 6 OP  =  10 OP

 72  =  10 OP - 6 OP

 4 OP  =  72

 OP  =  72/4

   =  18 cm

Example 2 :

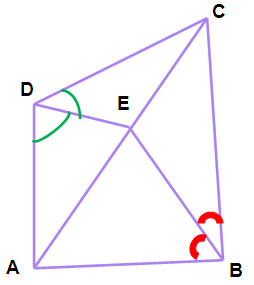
In a quadrilateral ABCD, the bisectors of ∠B and ∠D intersect on AC at E. Prove that (AB/BC) = (AD/DC).

Solution :

Here DE is the internal angle bisector of angle D.

by using internal bisector theorem, we get

(AE/EC)  =  (AD/DC)  ----- (1)

Here BE is the internal angle bisector of angle B.

(AE/EC)  =  (AB/BC)  ----- (2)

from (1) and (2) we get,

 (AB/BC)  =  (AD/DC)

Hence proved.

Example 3 :

The internal bisector of ∠A of triangle ABC meets BC at D and the external bisector of ∠A meets BC produced at E. Prove that (BD/BE)  =  (CD/CE).

Solution :

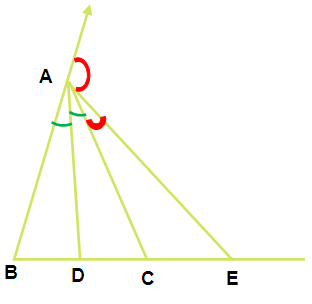
In triangle ABC, AD is the internal bisector of angle A.

by using angular bisector theorem in triangle ABC

(BD/DC)  =  (AB/AC) ----- (1)

In triangle ABC, AE is the internal bisector of angle A.

(BE/CE)  =  (AB/AC) ----- (2)

from (1) and (2) we get,

(BD/DC)  =  (BE/CE)

(BD/BE)  =  (DC/CE)

Hence proved.

Example 4 :

ABCD is a quadrilateral with AB = AD. If AE and AF are internal bisectors of ∠BAC and ∠DAC respectively,then prove that the sides EF and BD are parallel.

Solution:

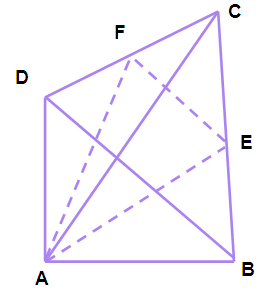
In triangle ABC, AE is the internal bisector of ∠BAC

by using bisector theorem, we get

(AB/AC)  =  (BE/EC)  ----- (1)

In triangle ADC, AF is the internal bisector of ∠DAC

by using bisector theorem, we get

(AD/AC)  =  (DF/FC)

Since lengths of AD and AB are equal, we may replace AB instead of AD.

(AB/AC)  =  (DF/FC)  ----- (2)

from (1) and (2) we get

(DF/FC)  =  (BE/EC)

So, EF and BD are parallel by using converse of "Thales theorem".

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.