SOLVING SPECIAL SYSTEMS
About "Solving special systems"
Solving special systems by graphing worksheet :
We can determine whether a system of linear equation has one solution, many solutions or no solution either by inspecting its graph or by solving it algebraically.
Solving special systems - Examples
Example 1 :
Solve the given system of equations by graphing.
x + y = 7
4x + 4y = 12
Solution :
Step 1 :
Write the given equations in slope-intercept form.
y = mx + b
x + y = 7
y = - x + 7
(slope is -1 and y-intercept is 7)
4x + 4y = 12
Divide both sides by 4.
x + y = 3
y = - x + 3
(slope is -1 and y-intercept is 3)
Based on slope and y-intercept, we can graph the given equations.
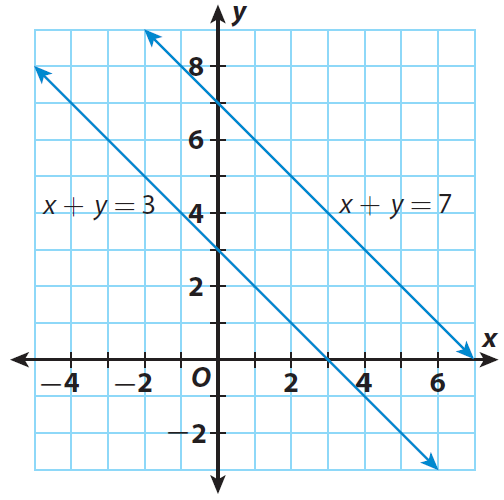
Step 2 :
In the above graph, the lines do not intersect. They appear to be parallel and and no points in common.
Does this linear system have a solution ? Use the graph to explain.
Since the lines are parallel and they do not intersect, there is no point of intersection. So, the system has no solution.
Reflection :
1. Can you conclude that the system of linear equation has no solution without graphing ?
Yes
We have to find the slopes and y-intercepts of the given two lines. If the slopes are equal, but y-intercepts are different, the lines will be parallel. Then, the system will not have solution.
2. Can you conclude that the system of linear equation has infinitely many solutions without graphing ?
Yes
We have to find the slopes and y-intercepts of the given two lines. If the slopes are equal and y-intercepts are also equal, both the equations represent the same line. All ordered pairs on the line will make both equations true and all points on the line are points of intersection.
Then, the system will have infinitely many solutions.
Example 2 :
Determine whether the system given below has one solution, infinitely many solutions or no solution.
x + y = 3
2x + 2y = 6
Solution :
Step 1 :
Write the given equations in slope-intercept form.
y = mx + b
x + y = 3
y = - x + 3
(slope is -1 and y-intercept is 3)
2x + 2y = 6
Divide both sides by 2.
x + y = 3
y = - x + 3
(slope is -1 and y-intercept is 3)
Step 2 :
The slopes of both the equations are same and y-intercepts are also same.
So, both the equations represents the same line. All ordered pairs on the line will make both equations true and all points on the line are points of intersection.
Hence, the system has infinitely many solutions.
Example 3 :
Solve the system of linear equations by substitution.
x - y = - 2
- x + y = 4
Solution :
Step 1 :
Solve the equation - x + y = 4 for "y".
- x + y = 4
Add "x" to both sides.
(-x + y) + x = (4) + x
-x + y + x = 4 + x
Simplify.
y = 4 + x
Step 2 :
Substitute y = 4 + x in the other equation.
x - y = - 2
x - (4+x) = -2
x - 4 - x = -2
Simplify.
-4 = -2
Step 3 :
Interpret the solution.
The result (-4 = -2) is the false statement. So there is no solution for the given system.
Example 4 :
Solve the system of linear equations by elimination.
2x + y = - 2
4x + 2y = - 4
Solution :
Step 1 :
2x + y = - 2 ------- (1)
4x + 2y = - 4 ------- (2)
In the given system, to eliminate one of the variables, the coefficients of that variable must be same and signs must be opposite.
The coefficients of the variable "x" are not same in both the equations and also the variable "y".
To make the coefficients of "y" same and signs opposite, multiply the first equation by -2.
(1) ⋅ 2 ------ > (-2)(2x + y) = (-2)(-2)
-4x - 2y = 4 ------- (3)
Step 2 :
Now, we can add equations (2) and (3) to eliminate the variable 2y.
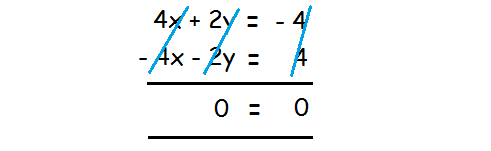
Step 3 :
Interpret the solution.
The result is the statement 0 = 0, which is always true.
So the system has infinitely many solutions.
After having gone through the stuff given above, we hope that the students would have understood "Solving special systems"
Apart from the stuff given above, if you want to know more about "Solving special systems", please click here
Apart from the stuff given on "Solving special systems", if you need any other stuff in math, please use our google custom search here.
WORD PROBLEMS
HCF and LCM word problems
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
