SOLVING QUADRATIC INEQUALITIES ALGEBRAICALLY
Solving Factorable Quadratic Inequalities
Solving Non-Factorable Quadratic Inequalities
Solved Problems
Solve the following quadratic inequalities.
Example 1 :
x2 + 5x + 6 ≥ 0
Solution :
x2 + 5x + 6 ≥ 0
(x + 2)(x + 3) ≥ 0 ----(1)
Assume the above inequality as equation and solve for x.
(x + 2)(x + 3) = 0
x = -2 or x = -3
Mark the two values -2 and -3 on the real number line and split up the real numbers into intervals as shown below.
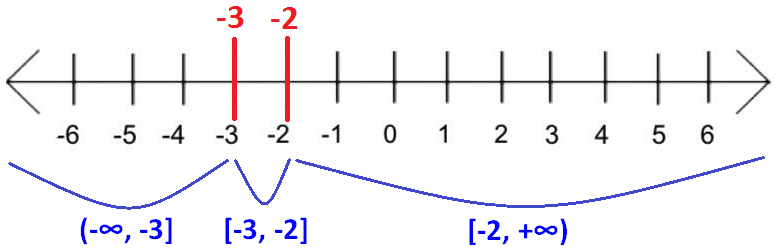
Testing the interval (-∞, -3] :
Take a random value in the interval (-∞, -3], say -4.
Substitute x = -4 into (1).
(-4 + 2)(-4 + 3) ≥ 0
(-2)(-1) ≥ 0
2 ≥ 0 (TRUE)
The interval (-∞, -3] satisfies the given inequality.
Testing the interval [-3, -2] :
Take a random value in the interval [-3, -2], say -2.5.
Substitute x = -2.5 for x into (1).
(-2.5 + 2)(-2.5 + 3) ≥ 0
(-0.5)(0.5) ≥ 0
-0.25 ≥ 0 (FALSE)
The interval [-3, -2] does not satisfy the given inequality.
Testing the interval [-2, +∞] :
Take a random value in the interval [-2, +∞), say 0.
Substitute x = 0 into (1).
(0 + 2)(0 + 3) ≥ 0
(2)(3) ≥ 0
6 ≥ 0 (TRUE)
The interval [-2, +∞) satisfies the given inequality.
Hence, the solution is
(-∞, -3] U [-2, +∞)
(or)
x ≤ -3 or x ≥ -2
Example 2 :
-x2 + 2x - 5 < 0
Solution :
-x2 + 2x - 5 > 0
Multiply both sides by -1.
-1(-x2 + 2x - 5) > -1(0)
x2 - 2x + 5 > 0
The quadratic expression (x2 - 2x + 5) is not factorable.
Write the corresponding quadratic function.
y = x2 - 2x + 5
x2 - 2x + 5 > 0 -----> y > 0 ----(1)
Find the value of the discriminant b2 - 4ac.
b2 - 4ac = (-2)2 - 4(1)(5)
= 4 - 20
= -16 < 0
Since b2 - 4ac < 0, the quadratioc function y = x2 - 2x + 5 has no zeros, that is, the parabola represented by the above quadratic function does not intersect x-axis. And also, the leading coefficient of the quadratic function is 1. So the parabola opens up.
Since the parabola opens up and it does not intersect x-axis, the parabola is above the x-axis. So, the y-coordinates in all the points on the parabola will be greater than zero and and x-coordinate can be any real number.
Therefore, (1) is true and the solution for the given quadratic inequality is all real numbers, that is x ∈ R.
Example 3 :
-x2 + 4 ≥ 0
Solution :
-x2 + 4 ≥ 0
Multiply both sides by -1.
-1(-x2 + 4) ≤ -1(0)
x2 - 4 ≤ 0
x2 - 22 ≤ 0
(x + 2)(x - 2) ≤ 0 ----(1)
Assume the above inequality as equation and solve for x.
(x + 2)(x - 2) = 0
x = -2 or x = 2
Mark the two values -2 and 2 on the real number line and split up the real numbers into intervals as shown below.
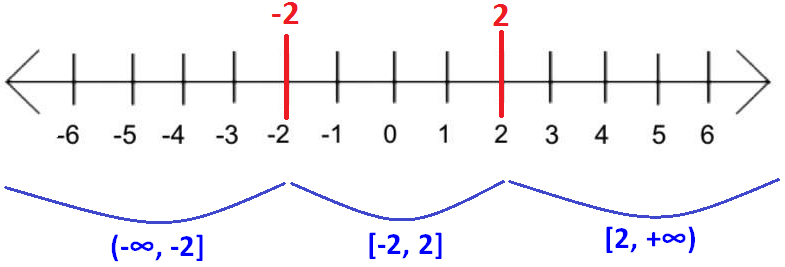
Testing the interval (-∞, -2] :
Take a random value in the interval (-∞, -2], say -3.
Substitute x = -3 into (1).
(-3 + 2)(-3 - 2) ≤ 0
(-1)(-5) ≤ 0
5 ≤ 0 (FALSE)
The interval (-∞, -2] does not satisfy the given inequality.
Testing the interval [-2, 2] :
Take a random value in the interval [-2, 2], say 0.
Substitute x = 0 into (1).
(0 + 2)(0 - 2) ≤ 0
(2)(-2) ≤ 0
-4 ≤ 0 (TRUE)
The interval [-2, 2] satisfies the given inequality.
Testing the interval [2, +∞] :
Take a random value in the interval [2, +∞), say 3.
Substitute x = 3 into (1).
(3 + 2)(3 - 2) ≤ 0
(5)(1) ≤ 0
5 ≤ 0 (FALSE)
The interval [2, +∞) does not satisfy the given inequality.
Hence the solution is
[-2, 2]
(or)
-2 ≤ x ≤ 2
Example 4 :
Solve the quadratic inequality given.
x2 + 4x +7 < 0
Solution :
x2 + 4x +7 < 0
The quadratic expression (x2 + 4x +7) is not factorable.
Write the corresponding quadratic function.
y = x2 + 4x +7
x2 + 4x +7 < 0 -----> y < 0 ----(1)
Find the value of the discriminant b2 - 4ac.
b2 - 4ac = 42 - 4(1)(7)
= 16 - 28
= -12 < 0
Since b2 - 4ac < 0, the quadratioc function y = x2 - 2x + 5 has no zeros, that is, the parabola represented by the above quadratic function does not intersect x-axis. And also, the leading coefficient of the quadratic function is 1. So the parabola opens up.
Since the parabola opens up and it does not intersect x-axis, the parabola is above the x-axis. So, the y-coordinates in all the points on the parabola will be greater than zero and and x-coordinate can be any real number.
Therefore, (1) is false and there is NO solution for the given quadratic inequality.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
