SOLVING SYSTEMS OF EQUATIONS IN THREE VARIABLES

Question 1 :

Solve the following system of linear equations in three variables

x + y + z = 5 ; 2x − y + z = 9 ; x − 2y + 3z = 16

Solution :

x + y + z = 5  -------(1)

2x − y + z = 9   -------(2)

x − 2y + 3z = 16   -------(3)

Let us add (1) and (2)

Multiply the first equation by 2 and add by (3)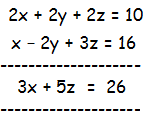

Let 3x + 2z  =  14  ----(4) and 3x + 5z = 26  ---(5)

(4) - (5) 

  3x + 2z  =  14

  3x + 5z  =  26

  (-)   (-)      (-)

  ----------------

      -3z  =  -12  ==> z  =  4

By applying z = 4 in (4), we get

3x + 2(4)  =  14

3x + 8  =  12

3x  =  14 - 8

3x  =  6  ==>  x  =  2

By applying x 2 and z = 4 in (1), we get 

2 + y + 4  =  5

6 + y  =  5 

y  =  5 - 6

y  =  -1

Hence the solution is

(x, y, z)  =  (2, -1, 2)

Question 2 :

(1/x) - (2/y) + 4  =  0

(1/y) - (1/z) + 1  =  0

(2/z) + (3/x)  =  14

Solution :

Let 1/x  =  a, 1/y = b and 1/z  = c

a - 2b  = -4  ----(1)

b - c = -1  ----(2)

3a + 2c  =  14  ----(3)

(1) + 2(2)  ==>  a - 2b + 0c =  -4

                      0a + 2b - 2c  =  -2

                      ---------------------

                           a - 2c  =  -6 ----(4)

(4) + (3)

      a - 2c  =  -6

     3a + 2c  =  14

    ----------------

         4a  =  8 ==>  a  =  2

By applying a = 2 in (4), we get

2 - 2c = -6

  -2c  =  -6 - 2

  -2c  =  -8  ==>  c  =  4

By applying the value of a in (1),

a - 2b  = -4  ----(1)

2 - 2b  =  -4

-2b  =  -4 -2

-2b  =  -6  ==>  b  =  3

Hence the solution is

(x, y, z)  =  (1/2, 1/3, 1/4)

Question 3 :

x + 20 = (3y/2) + 10  =  2z + 5  =  110 - (y + z)

Solution :

2z + 5  =  110 - (y + z)

2z + 5  =  110 - y - z

2z + z + y  =  110 - 5

3z + y  =  105  ----(3)

(1) + (2)

2x - 3y + 0z  =  -20

0x + 3y - 4z  =  -10 

------------------------

  2x - 4z  =  -30   ---(4)

(1)  ==>   2x - 3y + 0z  =  -20 

3(3)==>  0x + 3y + 9z  =  315

           ------------------------

             2x + 9z  =  295  ----(5)

(4) - (5)

  2x - 4z  =  -30

 -2x - 9z  =  -295

  -------------------

        -13z  =  -325

             z  =  25

By applying the value of z in (4), we get 

2x - 4(25)  =  -30

2x - 100  =  -30

2x  =  -30 + 100  =  70

x = 35

By applying the value of z in (3), we get

3(25) + y = 105

75 + y  =  105

y  =  105 - 75

y  =  30

Hence the solution is

(x, y, z)  =  (35, 30, 25)

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.