SOLVING WORD PROBLEMS USING VENN DIAGRAMS

Problem 1 :

In an examination 150 students secured first class in English or Math. Out of these 50 students obtained first class in both English and Math.  115 students secured first class in Math.  How many students secured first class in English only?

Solution :

n(E∪M)  =  150

n(E∩M)  =  50

n(M)  =  115

First we have to enter 50 in E∩M part

we have n(M) = 115.  

n(E∪M)  =  n(E) + n(M) - n(E∩M)

150  =  n(E) + 115 - 50

150  =  n(E) + 65

n(E)  =  150-65

n(E)  =  85

Only English  =  85-50

So, number of students who learn only English =  35

Problem 2 :

In a group of 30 persons, 10 take tea but not coffee. 18 take tea. Find how many take coffee but not tea, if each person takes at least one of the drinks?

Solution :

Given in a group of 30 persons, each one takes at least one of the drinks.

So, n(T∪C)  =  30 

n(T)  =  18

Also given that number of persons drink only tea is 10.

There fore, number of persons drink both tea and coffee 

n(T∩C)  =  n(T) - 10

=  18-10

=  8

Let x be the number of persons who drink at least one of the drinks.

From the above Venn diagram,

30  =  10 + 8 + x

x  =  30 - 18

x  =  12

Number of persons drink only coffee not tea is 12.

Problem 3 :

In a village there are 60 families.  Out of these 28 families speak only one language and 20 families speak other language. How many families speak both the languages?

Solution :

Let A and B be two languages.

n(A∪B)  =  60

n(A)  =  28, only n(A)  =  28-x

n(B)  =  20, only n(B)  =  20-x

Let x be the number of people who speak both language.

Number of people who speak atleast one of the language :

28-x+20-x+x  =  60

48-x  =  60

x  =  60-48

x  =  12

Number of families speak both the languages are 12.

Problem 4 :

In a school 150 students passed X standard Examination. 95 students applied for group I and 82 students applied for group II for the further studies. If 20 students applied neither of two, how many students applied for both groups?

Solution :

n(U)  =  150

n(A)  =  95

n(B)  =  82

n(A∪B)'  =  20

So, n(A∪B)  =  n(U) - n(A∪B)'

= 150 - 20

=  130

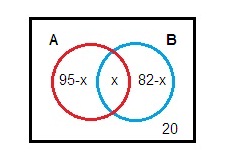
From the above Venn diagram 

(95-x) + x + (82-x)  =  130

95+82-x  =  130

x  =  177 - 130

x  =  47

Number of students applied for both the group is 47.

Problem 5 :

Sam is a section chief for an electric utility company. The employees in his section cut down tall trees or climb poles. Sam recently reported the following information to the management of the utility.

Out of 100 employees in my section, 55 can cut tall trees, 50 can climb poles, 11 can do both, 6 can't do any of the two. Is this information correct?

Solution :

n(U)  =  100

n(T∩P)  =  11

n(T∪P)'   =  6

n(T)  =  55

n(P)  =  50

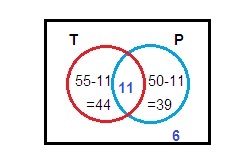
From the Venn diagram, we know that

n(U)  =  n(T∪P) + n(T∪P)'

 =  [44+11+39] + 6

=   100

So, the given information is correct.

Problem 6 :

A and B are two sets such that

n(A-B)  =  32+x, n(B-A)  =  5x and  n(A∩B)  =  x. 

Illustrate the information by means of a Venn diagram. Given that n(A) = n(B). Calculate

(i) the value of x  (ii) n(A∪B).

Solution :

n(A-B)  =  32 +x

n(B-A)  =  5x

n(A∩B)  =  x

n(A)  =  n(B)

some important results are

n(A)  =  n(A-B) + n(A∩B)

n(B)  =  n(B-A) + n(A∩B)

n(A∪B)  =  n(A-B) + n(A∩B) + n(B-A)

But given that n(A)  = n(B)

So, n(A-B) + n(A∩B) =  n(B-A) + n(A∩B)

n(A-B)  =  n(B-A)

32+x  =  5x

4x  =  32

(i)  x  =  8

(ii) n(A∪B)  =  n(A-B) + n(A∩B) + n(B-A)

=  32+x+x+5x

=  32+7x

=  32+7(8)

=  88

Problem 7 :

The following table shows the percentage of the students of a school who participated in Elocution and Drawing competitions.  

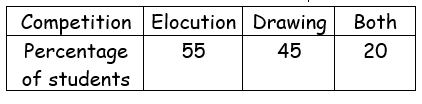
Draw a Venn diagram to represent this information and use it to find the percentage of the students who

(i)  participated in Elocution only

(ii) Participated in  Drawing only

(iii) Do not participate in any one of the competitions.

Solution :

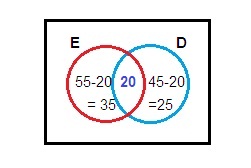
(i)  Participated in Elocution only  = 35

(ii) Participated in Drawing only   =  25

(ii) Do not participated in any one  of the competitions      

=  100-(35+20+25)

=  100-80

=  20

Problem 8 :

A village has total population 2500. Out of which 1300 use brand A soap and 1050 use brand B soap and 250 use both brands. Find the percentage of population who use neither of these soaps.

Solution :

n(U)  =  2500

n(A)  =  1300

n(B)  =  1050

n(A∩B)  =  250

We know that,

n(A∪B)  =  n(A) + n(B) - n(A∩B)

=  1300+1050-250

=  2100

n(A∪B)'   =  n(U) - n(A∪B)

=  2500-2100

=  400

Percentage of population who use neither of these soaps 

=  400/2500

=  0.16  x 100

=  16%

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.